Mise en Projet
Nous avons vu dans le chapitre précédant comment prendre en compte des choix simples et créer les structures de programmation adéquates afin de les gérer.
Il s'agira de voir dans ce chapitre comment aborder des situations plus complexes nécessitant de gérer plusieurs critères de choix, plusieurs conditions simultanément ainsi que leurs contraires.
Un test de 8 questions et 5 robots à programmer permettront de vérifier si cette étape importante de la programmation est bien maîtrisée.
ObjectifsÀ l'issue de ce chapitre, l'élève sera capable :
- de pouvoir gérer des situations de choix complexes faisant appel à plusieurs critères ou conditions;
- de pouvoir maîtriser l'inversion de ces conditions complexes;
- de pouvoir vérifier si des conditons complexes et leurs inverses sont correctes ou non;
- de mettre en œuvre les conditions complexes afin de gérer parfaitement les situations rencontrées.
 Quelques vidéos...
Quelques vidéos...
Ces quelques vidéos vont te présenter un résumé de ce qui suit.
| Booléens | de Morgan |
|---|---|
Quand on vérifie une condition, on est parfois amené à tenir compte de plusieurs critères simultanément. Par exemple :
La pelouse est mouillée s’il pleut OU si on l’arrose.
On parle alors d’expression logique ou booléenne. Le mot «booléen» vient du mathématicien, logicien et philosophe britannique George Boole qui a développé ce qu’on appelle l’algèbre de Boole, algèbre logique binaire basée sur la combinaison de seulement deux valeurs (puisque binaire) :
0 (ou FAUX) et 1 (ou VRAI)
Tout programmeur se doit de connaître quelques notions de base de l’algèbre de Boole s’il veut pouvoir construire des conditions prenant en compte plusieurs critères simultanément.
L'inventeur de l'algèbre binaire :

George Boole (1815-1864)
Par opérateur logique, on entend un élément de liaison que l'on va disposer entre deux ou plusieurs conditions. Par exemple, dans l'exemple ci-dessus
La pelouse est mouillée s’il pleut OU si on l’arrose,
l'opérateur logique est le OU du fait qu'il relie les deux conditions il pleut et on arrose (qui donneront chacune un résultat VRAI ou FAUX).
En programmation, les 3 opérateurs essentiels sont le ET, le OU et le NON ou PAS.
Passons en revue ces 3 opérateurs sous l'angle électrique (binaire, le courant passe ou ne passe pas), des ensembles, de l'équation et de la table de vérité.
1. L'opérateur logique ET.
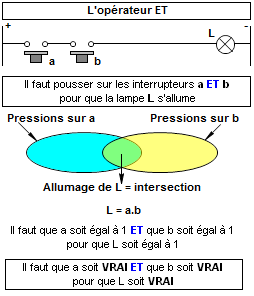
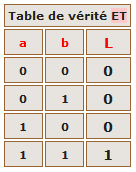
Une table de vérité est un tableau qui va donner le résultat de l'expression booléenne globale au vu des états VRAI (1) ou FAUX (0) de chacune des conditions qui la composent
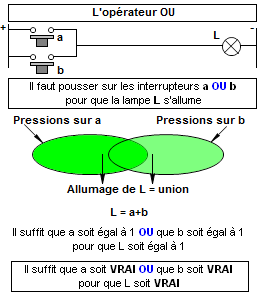
2. L'opérateur logique OU.
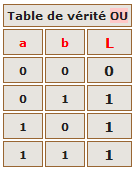
3. L'opérateur logique PAS.
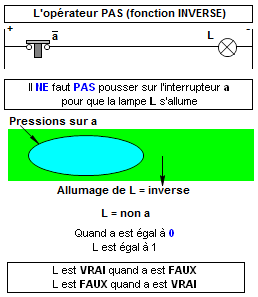
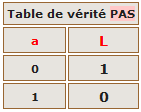
Il est parfois nécessaire ou pratique de pouvoir trouver rapidement l'inverse d'une expression booléenne.
C'est le mathématicien britannique de Morgan qui a énoncé les règles de négation des expressions booléennes.
Comme souvent, l'énoncé de la règle est plus difficile à comprendre qu'un exemple... Je vous laisse juge en vous présentant les deux. Les règles sont les suivantes :
La négation d'un ET devient un OU dans lequel chaque terme est inversé
La négation d'un OU devient un ET dans lequel chaque terme est inversé
Voici deux exemples concrets destinés à bien intégrer ces deux règles de négation.

Augustus de Morgan (1806-1871)
Commençons par la négation du ET :
je peux conduire si j'ai les clés de la voiture ET si j'ai mon permis
Quand ne puis-je pas conduire ? Voyons cela avec le schéma ci-dessous.

Donc, je ne peux pas conduire si je n'ai pas les clés OU si je n'ai pas mon permis.
Continuons avec la négation du OU :
la pelouse est mouillée quand il pleut OU qu'on l'arrose
Quand la pelouse est-elle sèche ? Voyons cela avec le schéma ci-dessous.
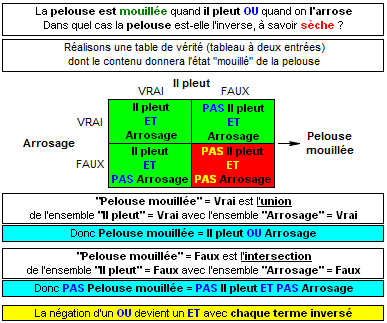
Donc, la pelouse est sèche s'il ne pleut pas ET si on ne l'arrose pas.
Quelques exercices vont permettre de bien ancrer tous ces concepts...