Objectifs
- Comprendre ce que sont les expressions booléennes;
- Prendre connaissance des 3 opérateurs logiques;
- Pouvoir construire les expressions booléennes comportant les opérateurs logiques adéquats.
Définition
Une expression booléenne est une suite d'éléments qui donneront, au final, un résultat true ou false.
Voici ci-dessous les principaux opérateurs de comparaison, quelques expressions booléennes et leurs résultats :
| == | Égal |
|---|---|
| != | Différent |
| > | Strictement supérieur |
| < | Strictement inférieur |
| >= | Supérieur ou égal |
| <= | Inférieur ou égal |
- - 2 == 3 qui donnera immuablement un résultat false;
- - 2 != 3 qui donnera immuablement un résultat true;
- - 2 + 2 == 4 qui donnera toujours un résultat true;
- - il pleut qui donnera un résultat true ou false en fonction des conditions météréologiques.
Tu as déjà utilisé des expressions booléennes sans le savoir dans les exercices précédents :
- - cotePile() qui vérifie si le côté visible de la pièce est pile (true) ou pas (false);
- - deviationGauche() qui vérifie s'il y a une déviation à gauche ou pas;
- - carteCarreau() qui vérifie si la carte tirée est du carreau ou pas;
- - bouleBleue() qui vérifie si la boule attrapée est bleue ou pas.
À ce stade, tu maîtrises donc déjà les expressions booléennes élémentaires. Naturellement, quand c'est simple, ce n'est pas gai :O)... Nous allons donc aller plus loin, voir comment il est possible de manipuler et associer des fonctions booléennes élémentaires. Ceci se fait grâce à 3 opérateurs logiques que nous allons passer en revue.
Les 3 opérateurs logiques
1. L'opérateur logique ET (&&)
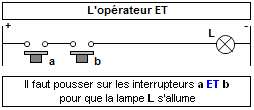
Comme le montre ce dessin, pour que la lampe s'allume (que le résultat de l'expression soit true), il faut enfoncer simultanément les boutons poussoirs a et b (il faut que la pression sur a soit true ET que la pression sur b soit true). Dans tous les autres cas, la lampe restera éteinte (le résultat de l'expression sera false).
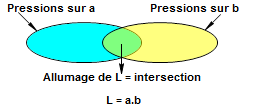
On remarque que l'ensemble des moments où la lampe L s'allume est l'intersection des moments où on pousse sur a et des moments où on pousse sur b.
En JavaScript, la syntaxe sera du style :
2. L'opérateur logique OU (||)
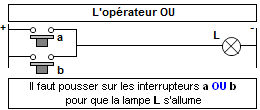
Comme le montre ce dessin, pour que la lampe s'allume (que le résultat de l'expression soit true), il faut enfoncer soit le bouton poussoir a, soit le bouton poussoir b (il faut que la pression sur a soit true OU que la pression sur b soit true). Si on pousse sur les deux boutons en même temps, la lampe sera également allumée. Si on ne pousse sur aucun bouton, la lampe restera éteinte (le résultat de l'expression sera false).
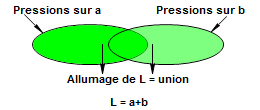
On remarque que l'ensemble des moments où la lampe L s'allume est l'union des moments où on pousse sur a et des moments où on pousse sur b.
En JavaScript, la syntaxe sera du style :
3. L'opérateur logique PAS (!)

Comme le montre ce dessin, pour que la lampe s'allume (que le résultat de l'expression soit true), il ne faut pas enfoncer le bouton poussoir a (il faut que la pression sur a soit false). Cet opérateur est appelé inverse ou négation car l'état de la lampe est l'inverse de l'état du bouton.
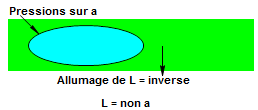
On remarque que l'ensemble des moments où la lampe L s'allume est l'inverse des moments où on pousse sur a.
En JavaScript, la syntaxe sera du style :
Construire des expressions booléennes
L'objectif des 5 prochains exercices et de te mettre en situation de construire des expressions booléennes faisant appel à ces opérateurs logiques.
Bonne découverte.