Cet exercice va s'intéresser à la mise en œuvre de deux boucles répétitives « for » imbriquées l'une dans l'autre, ce qui sera fort utile pour manipuler facilement les variables tableaux à deux dimensions.
Nous avons vu au premier exercice de ce chapitre que la boucle for est une boucle répétitive dans laquelle l'incrémentation du compteur est intégrée. Cette boucle tourne sur elle-même jusqu'à ce que la valeur limite soit atteinte.
Mais que se passe-t-il lorsque deux de ces boucles for sont imbriquées l'une dans l'autre ? À quel phénomène assiste-t-on ?
La boucle for intérieure va effectuer la totalité de son comptage pour chaque tour de la boucle extérieure. Prenons un exemple :
- for (i = 0; i < 3; i++)
- for (j = 0; j < 4; j++)
- instructionUnique;
La boucle i va tourner 3 fois (de 0 à 2 inclus) et, pour chaque tour de la boucle i, la boucle j va tourner 4 fois (de 0 à 3 inclus). Au final, la boucle j aura donc tourné 12 fois et l'instructionUnique sera donc effectuée 12 fois.
Mais quel intérêt ? Pourquoi ne pas prendre simplement un seule boucle for et la faire tourner 12 fois ?
Tout l'intérêt viendra de ce que pourra faire l'instructionUnique. Elle peut s'intéresser aux deux indices i et j en même temps, pour accéder à une case particulière d'un tableau à deux dimensions par exemple.
Nous verrons dans la synthèse de ce chapitre qu'il y a une particularité en JavaScript, le tableau à deux dimensions n'existe pas... Pour y arriver, nous créerons un tableau de tableaux. Mais ne nous attardons pas à ce détail, le but de cet exercice est de comprendre la manière dont les choses vont se passer globalement, nous nous intéresserons à la syntaxe JS plus tard, dans la synthèse.
Prenons l'exemple d'un tableau à 3 lignes (numérotées de 0 à 2) et à 4 colonnes (numérotées de 0 à 3) (il faut en effet savoir que tout tableau déclaré en JS démarre à l'indice 0, comme dans de nombreux autres langages). Graphiquement, ceci nous donnera la représentation suivante :
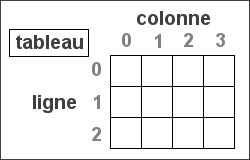
Nous pouvons alors reprendre les boucles for imbriquées ci-dessus pour initialiser toutes les cases de ce tableau à 0 par exemple. Nous transformerons l'instructionUnique en ceci :
- for (i = 0; i < 3; i++)
- for (j = 0; j < 4; j++)
- tableau [i][j] = 0;
Voici graphiquement comment va se dérouler l'accès aux différentes cases de ce tableau :
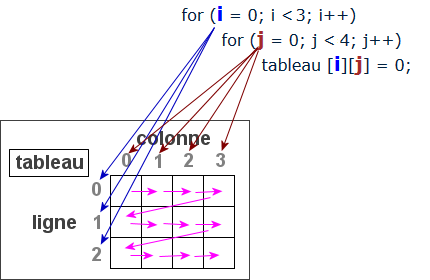
Étant donné que la boucle i est la plus extérieure et tourne donc le moins souvent, le tableau va se compléter ligne par ligne. Que se passerait-il si les deux boucles for étaient inversées, comme ceci ?
- for (j = 0; j < 4; j++)
- for (i = 0; i < 3; i++)
- tableau [i][j] = 0;
Voyons cela graphiquement :
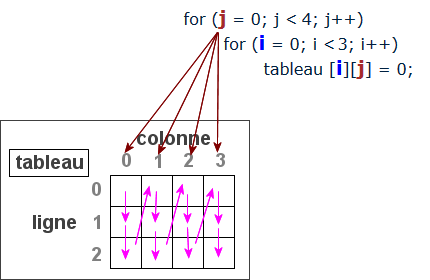
La boucle extérieure j, qui tourne le moins souvent, adresse les colonnes. Le tableau se remplira donc colonne par colonne contrairement au cas précédent.
Si tu as des difficultés à comprendre la différence entre ces deux variantes d'imbrication, le meilleur moyen est de prendre une feuille de papier et de faire deux lignes, l'une pour la variable i et l'autre pour la variable j. Note au fur et à mesure de l'exécution du code les valeurs que prennent ces deux variables et vois à quelles cases du tableau cela correspond.
Ta tâche, ton défi
De façon à bien intégrer l'importance dans la succession des boucles for, cet exercice double va te demander de compléter deux tableaux avec des jetons de couleur. À toi de découvrir comment organiser les boucles for imbriquées que tu vas utiliser afin d'effectuer ces deux tâches le plus aisément possible.
Voici le tableau contenant les jetons de couleur à placer.
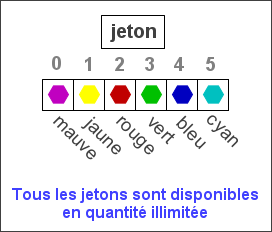
Et voici les 2 tableaux à compléter en positionnant les jetons correctement.
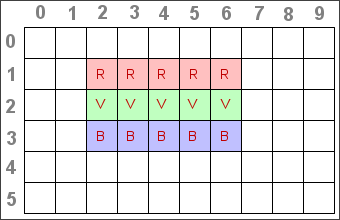
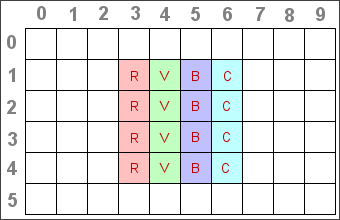
Pour chacun de ces tableaux, le robot doit placer dans les cases colorées les jetons correspondants, à savoir :
- Les jetons rouges dans les cases marquées R;
- Les jetons verts dans les cases marquées V;
- Les jetons bleus dans les cases marquées B;
- et les jetons cyan dans les cases marquées C.
Fais en sorte que, grâce à deux boucles for imbriquées, le robot place exactement les jetons adéquats partout où il le faut, sans débordement.
Pour réaliser sa tâche, le robot dispose d'une fonction d'action :
- placeJeton (numero, ligne, colonne); où numero est le numéro du jeton (de 0 à 5), ligne est le numéro de la ligne du tableau (de 0 à 5) et colonne est le numéro de la colonne du tableau (de 0 à 9) où placer ce jeton.
Pour cet exercice, le robot ne dispose pas de fonction de test
À toi de jouer afin d'arriver au remplissage correct des deux tableaux des façons les plus rationnelles possibles.
Bonne réalisation.