Objectives
- To grasp De Morgan's theorem on the negation of Boolean expressions containing « AND » or « OR »;
- To put the theorem into practice in the following exercises.
Explanations
When we have a Boolean expression containing « AND » or « OR », it is sometimes interesting to consider what the opposite would be. This means we must find the inverse of the Boolean expression.
DeMorgan examined this problem and found the solution. Rather than reinventing the wheel, let’s take advantage of his work to understand this problem.
1. The « AND » CASE
How do we go about finding the opposite of a Boolean expression containing « AND »?
The following is a flowchart showing situations in which we can or cannot drive: in order to drive, we need the keys « AND » a driver's license. In which cases can we not drive?
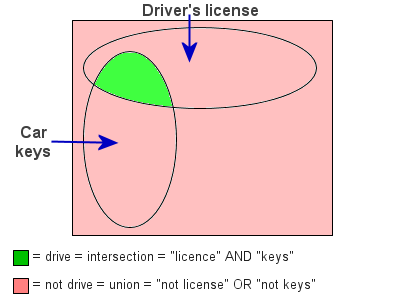
Therefore, the first part of DeMorgan's theorem becomes:
- The inverse of « AND » is « OR » with each term negated (inverted).
2. The « OR » CASE
How can we find the opposite of a Boolean expression containing « OR »?
Here is a flowchart showing situations in which the lawn is wet or dry: the lawn is wet if it's raining « OR » if it has been watered. In what case is the lawn dry?
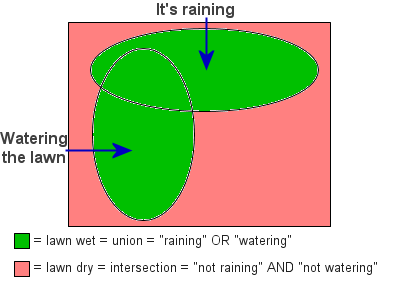
The second part of DeMorgan's theorem is therefore:
- The inverse of « OR » is « AND » with each term negated (inverted).
Your Turn
Now it's your turn to put the two parts of the theorem into practice in the following two exercises.
Good luck.