Fonctions périodiques et séries de Fourier
Nous présentons ici le formalisme général des fonction périodiques en plusieurs variables et de leur développement en série de Fourier.
1. Fonctions périodiques en une variable
Une fonction $f(x)$ est périodique de période $a$ ($a \gt 0$) si $$\begin{array} {ll} f(x+a)=f(x), & \forall x \in \mathbb{R}\end{array}$$ ou, de manière équivalente, si $$\begin{array} {ll} f(x+ka)=f(x), & \forall x \in [0, a], \forall k \in \mathbb{Z}.\end{array} \tag{1}$$ Une fonction périodique avec un suffisamment bon comportement peut être développée en série de Fourier : $$f(x)=\sum_{n \in \mathbb{Z}} c_n e^{inbx} ,~~~ b = 2 \pi / a$$ où les coefficients de Fourier sont donnés par la formule $$c_n = \dfrac 1 a \int_0^a e^{-inbx}f(x)~\dif x. \tag{2}$$
Remarque : On constate que rien ne change si, dans la formule (1), on remplace l'intervalle $[0, a]$ par l'intervalle $[-a/2, a/2]$ et, si dans la formule (2), on intègre entre $-a/2$ et $a/2$ plutôt qu'entre $0$ et $a$.
Exemple : L'onde carrée $$f(x)= \begin{cases} 0 & \mbox{si } -a/2 \lt x \lt 0 \\ 1 & \mbox{si } 0 \lt x \lt a/2\end{cases} $$ a pour coefficients de Fourier $$c_0=1/2$$ et $$c_n= i \dfrac{(-1)^n-1}{2n\pi}~~(n \ne 0).$$
2. Fonctions périodiques en plusieurs variables : cas particulier
Une fonction définie dans le plan ou dans l'espace peut être périodique en plus d'une variable. Nous donnerons ici les détails pour le cas de deux variables ; la généralisation au cas de trois variables est vue plus bas.
Commençons par le cas le plus simple : celui d'une fonction $f(x, y)$ pour laquelle il existe deux nombres positifs $a_1$ et $a_2$ tels que $$\begin{array} {ll} f(x+a_1, y)=f(x, y+a_2)=f(x, y), & \forall x, y \in \mathbb{R}.\end{array}$$ On pourra caractériser cette fonction de manière équivalente par le fait que $$\begin{array} {c} f(x+k a_1, y+l a_2)=f(x, y),~~~~~~~~~~~~~~~~~~~~~~~~~~ \\ ~~~~~~~~~~ \forall (x, y) \in [0, a_1] \times [0, a_2], \forall k, l \in \mathbb{Z}.\end{array} \tag{3}$$ De nouveau, si elle a un suffisamment bon comportement, une telle fonction pourra être développée en série de Fourier double : $$f(x, y)=\sum_{m,n \in \mathbb{Z}} c_{mn} e^{i(mb_1x+nb_2y)} ,~~~ b_j = 2 \pi / a_j$$ où les coefficients sont calculés selon la formule $$\mkern -30mu c_{mn} = \dfrac 1 {a_1a_2} \iint_{[0, a_1] \times [0, a_2]} e^{-i(mb_1x+nb_2y)}f(x, y)~\dif x\dif y. \mkern -5mu \tag{4}$$
Remarque : Ici encore, rien ne change si, dans les formule (3) et (4), on remplace le rectangle $[0, a_1] \times [0, a_2]$ par le rectangle $R=[-a_1/2, a_1/2] \times [-a_2/2, a_2/2]$.
On peut mettre les résultats précédents sous une forme vectorielle qui nous préparera au cas général. Définissons le vecteur position $\vec{x}=(x, y)$ et les vecteurs de base $$\begin{array} {ll} \vec{a}_1 = (a_1, 0), & \vec{a}_2 = (0, a_2). \end{array} $$ Les vecteurs de la forme $$\begin{array} {ll} \vec{l} = k \vec{a}_1 + l \vec{a}_2, & k, l \in \mathbb{Z} \end{array} $$ forment ce qu'on appelle un réseau¹, que nous noterons $\Lambda$. La définition de la périodicité pour $f$ peut alors s'écrire $$\begin{array} {ll} f(\vec{x}+\vec{l}) = f(\vec{x}) & \forall \vec{x} \in R,~\forall \vec{l} \in \Lambda \end{array} $$
Définissons aussi les vecteurs réciproques de base $$\begin{array} {ll} \vec{b}_1 = (b_1, 0), & \vec{b}_2 = (0, b_2). \end{array} $$ (On notera qu'ils sont complètement déterminés par la propriété $\vec{b}_j \cdot \vec{a}_k = 2 \pi \delta_{jk}$.) Les vecteurs de la forme $$\begin{array} {ll} \vec{g} = m \vec{b}_1 + n \vec{b}_2, & m, n \in \mathbb{Z} \end{array} $$ forment le réseau réciproque de $\Lambda$, noté $\Lambda^*$. Les formules pour les séries de Fourier peuvent alors s'écrire $$f(\vec{x})=\sum_{\vec{g} \in \Lambda^*} c_{\vec{g}} e^{i\vec{g} \cdot \vec{x}} \tag{5}$$ où, en désignant par $A$ l'aire du rectangle $R$, $$\mkern -30mu c_{\vec{g}} = \dfrac 1 {A} \iint_{R} e^{-i\vec{g} \cdot \vec{x}}f(\vec{x})~\dif^2 x. \mkern -5mu$$
¹ Techniquement, le type de réseau dont on parle ici porte dans la littérature le nom de réseau de Bravais.
3. Fonctions périodiques en plusieurs variables : cas général
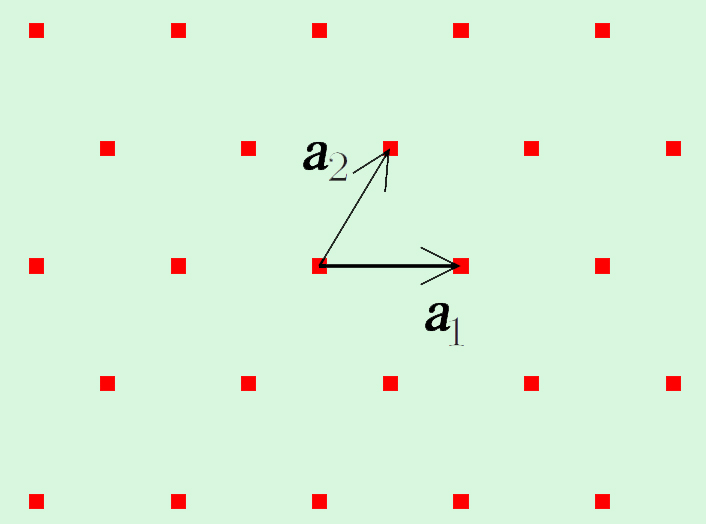
Passons maintenant au cas général pour une périodicité en deux variables : il existe deux vecteurs linéairement indépendants $\vec{a}_1$ et $\vec{a}_2$ tels que $$\begin{array} {l} f(\vec{x}+\vec{a}_1) = f(\vec{x}+\vec{a}_2) \\= f(\vec{x}),~~\forall \vec{x} \in \mathbb{R}^2.\end{array}$$
Exemple. On obtient ce qu'on appelle un réseau hexagonal (fig. 1) si on prend $$\begin{array} {lll} \vec{a}_1 = (a, 0), & \vec{a}_2 = (a/2, a\sqrt{3}/2), & (a \gt 0). \end{array} $$
On peut se ramener au cas particulier de la section précédente en effectuant le changement de variables $$\begin{array} {ll} \vec{x}=s\vec{a}_1+t\vec{a}_2, & f(\vec{x}) = h(s, t)~:\end{array} \tag{6}$$ la fonction $h(s, t)$ a alors la propriété $$\begin{array} {ll} h(s+1, t)=h(s, t+1)=h(s, t), & \forall s, t \in \mathbb{R}. \end{array}$$ On peut donc la développer en série de Fourier $$h(s, t)=\sum_{m,n \in \mathbb{Z}} c_{mn} e^{i(ms+nt)2\pi}, \tag{7}$$
où les coefficients sont donnés par $$c_{mn} = \int_0^1 \int_0^1 e^{-i(ms+nt)2\pi}h(s, t)~\dif s\dif t. \tag{8}$$Remarque. Pour simplifier, on supposera que les deux
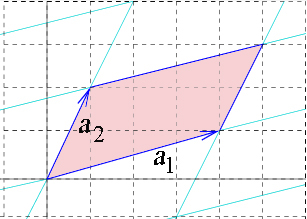
réseau plan quelconque.
vecteurs sont numérotés de telle manière que le jacobien de la transformation (6), $$A = \det \dfrac{\partial(x, y)}{\partial(s, t)}= \begin{vmatrix} a_{1x} & a_{2x} \\ a_{1y} & a_{2y} \end{vmatrix},$$ soit positif. On pourra alors interpréter $A$ également comme l'aire du parallélogramme (représenté à la fig. 2) $$M_B = \{\vec{x}=s\vec{a}_1+t\vec{a}_2 |~0 \le s, t \le 1\}.$$ On appelle le parallélogramme $M_B$ la maille de base.
du réseau de la fig. 1.
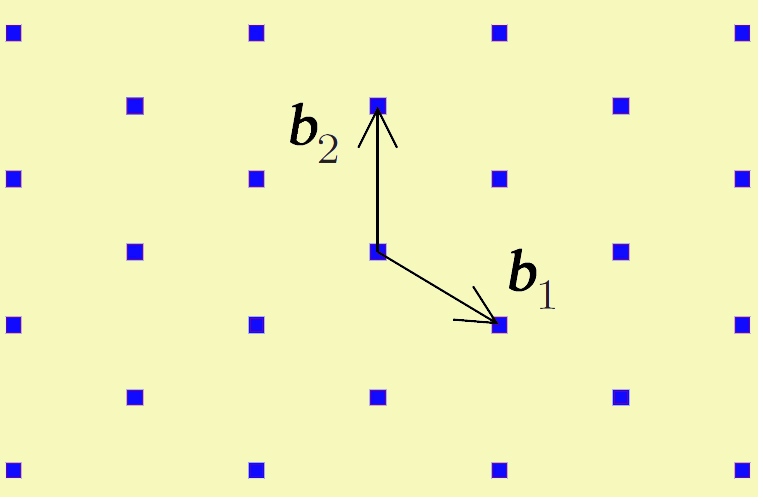
Introduisons maintenant les vecteurs réciproques de base $\vec{b}_1$ et $\vec{b}_2$ : ils sont définis par la propriété² $$\mkern -30mu \vec{b}_j \cdot \vec{a}_k = 2 \pi \delta_{jk}. \mkern -40mu \tag{9}$$ Remarquons que dans les formules (7) et (8), on peut introduire les vecteurs du réseau réciproque pour écrire $$\begin{array} {ll} (ms+nt)2\pi=\vec{g}\cdot\vec{x}, & \vec{g}=m\vec{b}_1+n\vec{b}_2. \end{array}$$ En remplaçant la notation $c_{mn}$ par $c_{\vec{g}}$, (7) redonne immédiatement (5) et, en revenant aux variables de départ dans (8), on obtient pour les coefficients de Fourier $$c_{\vec{g}} = \dfrac 1 {A} \iint_{M_B} e^{-i\vec{g} \cdot \vec{x}}f(\vec{x})~\dif^2 x. \tag{10}$$
² Si on résout le système (9), on obtient très facilement $\vec{b}_1 = \dfrac {2\pi} A (a_{2y}, -a_{2x})$ et $\vec{b}_2 = \dfrac {2\pi} A (-a_{1y}, a_{1x})$.
4. Maille de Wigner-Seitz et zone de Brilloin
Dans un réseau (pour simplifier, nous nous limiterons à un réseau plan), on désigne sous le nom de maille primitive n'importe quelle portion du plan « d'un seul morceau » $M_P$ qui satisfait les conditions :
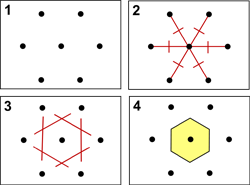
Wigner-Seitz pour un réseau hexagonal
.
- l'ensemble des parties du plan obtenues en translatant $M_P$ par un vecteur du réseau donne le plan au complet ;
- deux parties du plan obtenues en translatant $M_P$ par des vecteurs différents du réseau ont au plus en commun des points sur leurs bords.
Un exemple de maille primitive est fourni par la maille de base de la section précédente. On peut aussi construire une maille primitive en considérant la partie du plan qui est plus proche de l'origine que de tout autre point du réseau (voir fig. 3). Cette maille porte le nom de maille de Wigner-Seitz.
On peut montrer que toutes les mailles primitives ont la même aire et que dans la formule (10), l'intégration peut être effectuée sur n'importe quelle maille primitive, pas nécessairement sur la maille de base.
La maille de Wigner-Seitz joue un rôle particulièrement important dans les réseaux réciproques, où elle porte le nom de (première) zone de Brilloin.
5. Notes et références
On pourra trouver la théorie de base des réseaux et des réseaux réciproques dans n'importe quel bon livre d'introduction à la physique de l'état solide, comme par exemple J.M. Ziman. Principles of the theory of solids. 2nd edition. Cambridge University Press. 1972.
Fonctions périodiques en trois variables
Le cas des fonctions périodiques en trois variables se traite de manière similaire à ce qu'on a vu dans la section 3. Supposons qu'on ait une fonction $f(\vec{x})$, où $\vec{x}=(x, y, z)$, et trois vecteurs linéairement indépendants $\vec{a}_1$, $\vec{a}_2$ et $\vec{a}_3$ tels que $$\begin{array} {ll} f(\vec{x}+\vec{a}_1) = f(\vec{x}+\vec{a}_2) = f(\vec{x}+\vec{a}_3)= f(\vec{x}), &\forall \vec{x} \in \mathbb{R}^3.\end{array}$$ En effectuant le changement de variable $$\begin{array} {ll} \vec{x}=s\vec{a}_1+t\vec{a}_2+u\vec{a}_3, & f(\vec{x}) = h(s, t, u), \end{array} \tag{11}$$ on se ramène à une fonction $h(s, t, u)$ qui est périodique en chacune de ses variables et qu'on peut développer en série de Fourier triple.
Le jacobien de la transformation (11) est $$V= \det \dfrac{\partial(x, y, z)}{\partial(s, t, u)} = \begin{vmatrix} a_{1x} & a_{2x} & a_{3x} \\ a_{1y} & a_{2y} & a_{3y} \\ a_{1z} & a_{2z} & a_{3z} \end{vmatrix} = \vec{a}_1 \cdot (\vec{a}_2 \times \vec{a}_3).$$ Le signe de $V$ dépend de l'ordre des vecteurs de base. Si on les numérote de manière à ce que le résultat soit positif, $V$ représente alors le volume de la maille de base, qui est le parallélépipède $$M_B = \{\vec{x}=s\vec{a}_1+t\vec{a}_2+u\vec{a}_3 |~0 \le s, t, u \le 1\}.$$
En introduisant les vecteurs réciproques de base $$\begin{array} {lll} \vec{b}_1 = \dfrac {2\pi} V \vec{a}_2 \times \vec{a}_3, & \vec{b}_2 = \dfrac {2\pi} V \vec{a}_3 \times \vec{a}_1, & \vec{b}_3 = \dfrac {2\pi} V \vec{a}_1 \times \vec{a}_2 \end{array}$$ et les vecteurs de réseau réciproque $$\begin{array} {lll} \vec{g}= n_1\vec{b}_1 +n_2\vec{b}_2 +n_3\vec{b}_3 & (n_1, n_2, n_3 \in \mathbb{Z}), \end{array}$$ on peut donner la forme simple suivante au développement en série de Fourier de $f(\vec{x})$ : $$\begin{array} {ll} f(\vec{x})=\displaystyle\sum_{\vec{g} \in \Lambda^*} c_{\vec{g}} e^{i\vec{g} \cdot \vec{x}}, & c_{\vec{g}} = \dfrac 1 {V} \displaystyle\iiint_{M_B} e^{-i\vec{g} \cdot \vec{x}}f(\vec{x})~\dif^3 x. \end{array}$$