Mise en projet
Avant de nous intéresser à la façon dont l'ordinateur calcule, il est intéressant de voir comment peuvent se dérouler les 4 opéations de base en binaire. Cela permettra d'expliquer l'architecture de l'UAL.
Les 4 opérations de base en binaire
L'addition
Intéressons-nous d'abord à l'addition décimale. Les chiffres sont additionnés dans chaque rang. Lorsqu'il y a un dépassement de capacité du rang (nombre supérieur à 9), on reporte l'excès sur le rang précédent, qui a un exposant de 10 supérieur d'une unité. La valeur reportée est donc divisée par 10 pour garder l'égalité. Voyons cela avec l'addition de 3 nombres décimaux.
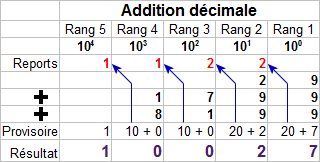
Addition décimale avec reports
Le principe sera exactement le même pour l'addition binaire sinon qu'on travaille maintenant avec des puissances de 2. Lorsqu'il y a un dépassement de capacité du rang (nombre supérieur à 1), l'excès est reporté sur le rang précédent qui a un exposant de 2 supérieur d'une unité. La valeur reportée est donc divisée par 2 pour garder l'égalité. Voyons un exemple concret avec l'addition de 2 nombres binaires.
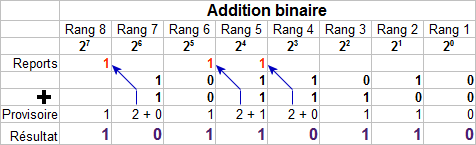
Addition binaire avec reports
La soustraction
Le principe de la soustraction décimale est assez semblable à celui de l'addition. La différence est que, quand le chiffre dont on soustrait est insuffisant, on puise une unité dans le rang supérieur, ce qui permet d'ajouter 10 dans le rang dont on s'occupe.
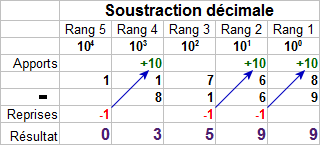
Soustraction décimale avec reprises
La soustraction binaire se déroule selon le même principe, sinon que la reprise d'une unité au rang supérieur permet d'ajouter 2 au rang dont on s'occupe.
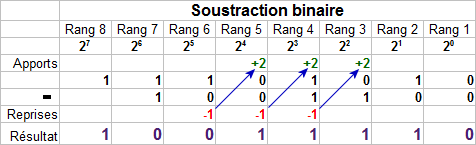
Soustraction binaire avec reprises
Question : y aurait-il moyen de transformer une soustraction en addition ?
La soustraction magique
Grâce à une astuce, il y a effectivement moyen de transformer une soustraction en addition. Voyons d'abord cela en décimal pour faciliter la compréhension de ce subterfuge.
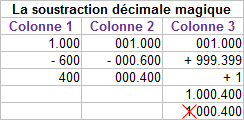
Soustraction décimale "magique".
Dans la colonne 1, la soustraction est habituelle. Le résultat est 400.
Dans la colonne 2, grâce à des zéros non significatifs, nous égalisons les rangs des deux nombres à 6 rangs par exemple, ce qui ne change rien au calcul. La soustraction donne le résultat attendu.
Dans la colonne 3, nous appliquons le subterfuge, à savoir :
- Nous égalisons les 2 nombres à 6 rangs par exemple;
- Nous effectuons le complément à 9 du nombre à soustraire, c'est-à-dire que nous remplaçons chacun de ses chiffres par la valeur qui manque pour obtenir 9;
- Nous ajoutons en plus la valeur 1;
- Nous additionnons le tout;
- Et nous tronçonnons du résultat tout ce qui dépasse le nombre de rangs fixé au départ;
- Résultat : nous obtenons la même valeur que le résultat attendu par la soustraction.
Mais pourquoi tout cela ? Parce que nous gagnons un circuit électronique. Au lieu d'avoir deux circuits distincts, l'un pour les additions et l'autre pour les soustractions, nous pouvons effectuer les deux opérations avec le même circuit électronique. Car cette astuce est valable également en binaire.
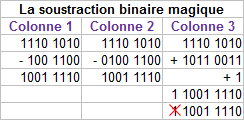
Soustraction binaire "magique".
Le processus est le même, à la subtilité de la base 2 au lieu de 10. Voici les calculs de la colonne 3 :
- Égalisation des rangs au nombre de fils du bus (ici, 8);
- Complément à 1 du nombre à soustraire (les 0 remplacés par des 1 et inversément);
- Addition en ajoutant encore 1;
- Non prise en compte du débordement du bus, et le tour est joué.
Passons à l'opération suivante.
La multiplication
En décimal comme en binaire, la multiplication est une addition en tenant compte des rangs du multiplicateur. Examinons en détail l'opération décimale 413 x 25 :
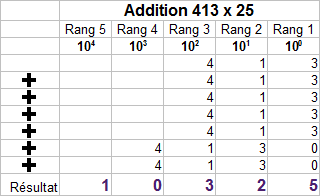
Multiplication décimale transformée en addition par décalage de rangs.
Le résultat est obtenu en additionnant le multiplicande 5 fois dans le rang 1 et 2 fois dans le rang 2. L'opération est strictement identique en binaire.
Chouette, la multiplication peut se transformer en addition par simple décalage de rangs.
La division
Entrer dans les détails de la division nous emmènerait au-delà du propos de ce chapitre mais, en extrapolant, on peut imaginer que la division soit une soustraction en tenant compte des rangs. Par les astuces cumulées de l'addition compémentaire et du changement de rangs, la division pourra être ramenée à une suite d'additions.
Finalement...
...l'unité arithmétique va pouvoir se résumer à un additionneur flanqué de petits circuits capables de :
- Changer les 0 en 1 et inversément;
- Décaler les rangs.
Constitution de l'additionneur binaire
Constater que les 4 opérations de base peuvent se résumer à une addition est très bien, mais comment réaliser une addition de courants électriques qui réponde aux règles de l'algèbre binaire ? Examinons la table de vérité suivante (une table de vérité est l'état que doivent prendre les sorties Somme et Report en fonction de l'état des entrées a et b).
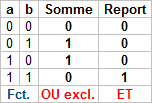
Table de vérité du demi-additionneur.
La table de vérité montre que le Report nécessite une fonction logique ET : il n'y a du courant en sortie QUE s'il y a du courant simultanément sur a ET b.
Cette table montre également que la Somme nécessite une fonction logique OU exclusif : Il n'y aura du courant en sortie QUE s'il y a du courant SOIT sur a SOIT sur b.
Ces fonctions logiques sont réalisées grâce à des composants électroniques (transistors,...). Pour 2 fils en entrée, le système va donc se présenter comme suit pour chaque fil du bus de données :
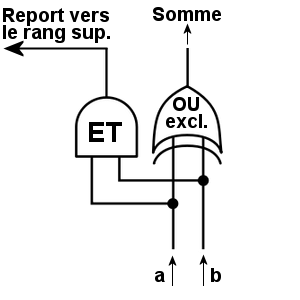
Schéma logique du demi-additionneur.
On parle de demi-additionneur car on comprend que ce système fonctionne sans tenir compte d'un report pouvant provenir du rang inférieur. L'additionneur complet devra, en conséquence, être pourvu de trois fils en entrée, comme ceci :
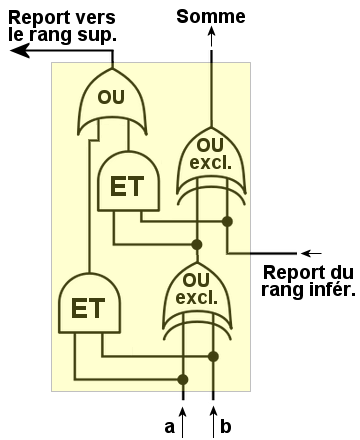
Schéma logique de l'additionneur complet.
Cela peut paraître compliqué, mais il s'agit simplement de deux demi-additionneurs mis bout à bout complétés d'une fonction OU sur les reports. Les plus passionné.e.s d'entre vous pourront vérifier si le schéma logique donne un résultat conforme à la table de vérité suivante :
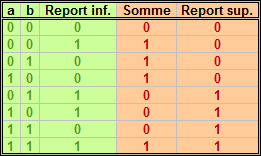
Table de vérité de l'additionneur complet.
Pour un bus de données de 8 fils, l'UAL va se présenter schématiquement comme ceci :
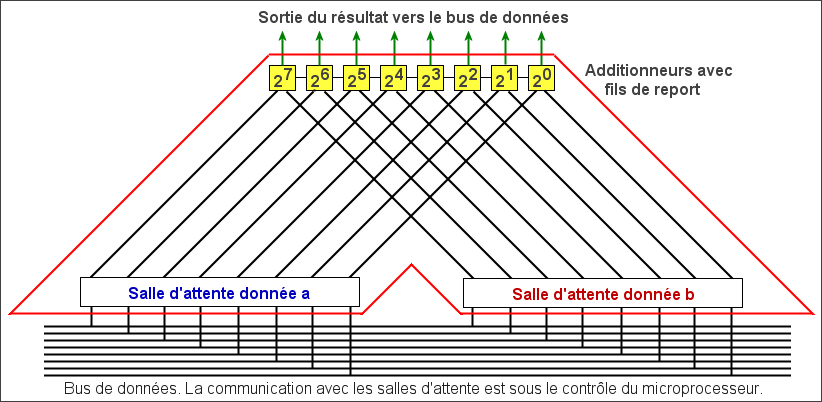
Schéma général de l'UAL.
Nous verrons plus en profondeur le fonctionnement de cette UAL dans un chapitre ultérieur, mais nous pouvons déjà en dire un petit mot :
- Les données a et b sont amenées l'une après l'autre dans leurs salles d'attente;
- Lorsque les données sont prêtes, le microprocesseur envoie la commande de l'opération à réaliser (addition, comparaison,...)
- En cas d'opération arithmétique, le résultat sort et retourne vers le bus de données afin d'être utilisé là où c'est prévu;
- En cas de comparaison (voir ci-dessous), un fil particulier informe le microprocesseur du résultat du test qui est soit vrai ou faux.
Et l'unité logique...???
L'unité logique va amener deux données dans les "salles d'attente" et vérifier si elles sont égales ou non. L'UAL est utilisée chaque fois que, dans votre programme ou code, vous testez une condition.
Continuons maintenant notre exploration.