Sommes et notation Σ
Calculs de sommes
L'intégrale, on va le voir, est définie comme une limite de sommes. Pour être capable de calculer au moins l'intégrale des fonctions les plus simples, il est donc nécessaire de se familiariser avec le calcul des sommes, ce qui est l'objet ce cette section.
Une version plus détaillée est fournie dans le document PDF dont le lien est fourni plus bas, mais voici un résumé des résultats principaux.
Définition. Soient \(m\) et \(n\) des nombres entiers avec \(m\lt n\). Si \(a_{m}\), \(a_{m+1}\), \(a_{m+2}\), … , \(a_{n-1}\), \(a_{n}\) sont des nombres réels, on désigne leur somme par le symbole \(\sum_{k=m}^n a_k \) : \[\sum_{k=m}^n a_k = a_{m}+a_{m+1}+a_{m+2}+ … +a_{n-1}+a_{n}.\] Les \(a_k\) sont appelés les termes de la somme et \(k\) est appelé l’indice de sommation.
Remarque. Le symbole Σ est la lettre grecque « sigma » majuscule. Le sigma correspond à notre s, qui est la première lettre du mot « somme ».
Le théorème suivant donne deux résultats fondamentaux concernant les sommes. Ces deux résultats sont importants, car ils vont se refléter dans des résultats similaires concernant les intégrales.
Théorème. On a :
- \(\sum_{k=m}^n ca_k = c\sum_{k=m}^n a_k\) ;
- \(\sum_{k=m}^n (a_k+b_k) = \sum_{k=m}^n a_k+\sum_{k=m}^n b_k\).
Finalement, la proposition qui suit permet de calculer les intégrales des fonctions linéaires, quadratiques et cubiques.
Proposition. On a :
- \(\sum_{k=1}^n 1 = n\) ;
- \(\sum_{k=1}^n k=\frac{n(n+1)}{2}\) ;
- \(\sum_{k=1}^n k^2=\frac{n(n+1)(2n+1)}{6}\) ;
- \(\sum_{k=1}^n k^3=\frac{n^2(n+1)^2}{4}\).
Pour plus de détails et pour les preuves du théorème et de la proposition, veuillez consulter le document PDF Sommes et notation Σ.
Vidéos
Voici quatre vidéos qui reprennent la théorie des sommes et qui présentent des exemples. Vous pouvez les visionner en plein écran (pour revenir à cette page web, poussez la touche Esc/Échap).
Exercices : sommes polynomiales
Une classe de sommes qui jouent un grand rôle en mathématiques est celle qui fait intervenir des puissances de l'indice. Voici tout d'abord quelques exercices pour vous familiariser avec leur calcul.
Exercice 1. Calculez a) $\sum_{i=251}^{750}1$; b) $\sum_{i=251}^{750}5$;
c) $\sum_{i=1}^{250}i$; d) $\sum_{i=1}^{750}i$; $ e)\sum_{i=251}^{750}i$; f) $\sum_{i=251}^{750}2i$.
g) $\sum_{i=1}^{250}(i+i^2)$ h) $\sum_{i=1}^{750}(i+i^2)$; k) $\sum_{i=251}^{750}(i+i^2)$.
Exercice 2. Trouvez l'expression de chacune des sommes suivantes en fonction de $n$ :
a) $\sum_{i=50}^{n}i$; b) $\sum_{i=100}^{2n}i^2$; c) $\sum_{i=1}^{n}(3i+1)^2$;
d) $\sum_{i=10}^{750}k^2$; e) $\sum_{i=n}^{2n}2i^3$.
Exercice 3. Trouvez l'expression de chacune des sommes suivantes en fonction de $n$ : a) $\sum_{i=50}^{n}i-\sum_{j=50}^{n}j$; b) $\sum_{i=1}^{n}2i+\sum_{j=1}^{n}(2j+1)$; c) $\sum_{i=1}^{n}(3i+1)-\sum_{k=1}^{n}3k$.
Exercice 4. Trouvez l'expression de chacune des sommes suivantes en fonction de $n$ : a) $\sum_{i=1}^{n}i+\sum_{i=n+1}^{2n}i$; b) $\sum_{i=5}^{n}(7i+5)+\sum_{i=5}^{n}(3i-5)$; c) $\sum_{i=5}^{n}i^2-\sum_{j=1}^{n}j^2$.
Les exercices suivants vont maintenant vous monter comment trouver les formules pour calculer ce type de sommes.
Exercice 5. a) Montrez qu'on a
$\sum_{k=1}^{n}[(k+1)^2-k^2]=(n+1)^2-1$.
b) Utilisez le fait que $(k+1)^2-k^2=2k+1$ pour montrer que
$\sum_{k=1}^{n}[(k+1)^2-k^2]=2\sum_{k=1}^{n}k+n$.
c) Montrez qu'on peut conclure de a) et b) que
$\sum_{k=1}^{n}k=\dfrac{n(n+1)}{2}$.
Exercice 6. a) Montrez qu'on a
$\sum_{k=1}^{n}[(k+1)^3-k^3]=(n+1)^3-1$.
b) Utilisez le fait que $(k+1)^3-k^3=3k^2+3k+1$ pour montrer que
$\sum_{k=1}^{n}[(k+1)^3-k^3]=3\sum_{k=1}^{n}k^2+\dfrac{n(3n+5)}{2}$.
c) Montrez qu'on peut conclure de a) et b) que
$\sum_{k=1}^{n}k^2=\dfrac{n(n+1)(2n+1)}{6}$.
Exercice 7. a) Montrez qu'on a
$\sum_{k=1}^{n}[(k+1)^4-k^4]=(n+1)^4-1$.
b) Utilisez le fait que
$(k+1)^4-k^4=4k^3+6k^2+4k+1$
pour montrer que
$\sum_{k=1}^{n}[(k+1)^2-k^2]=4\sum_{k=1}^{n}k^3+n(2n^2+5n+4)$.
c) Montrez qu'on peut conclure de a) et b) que
$\sum_{k=1}^{n}k^3={\left(\dfrac{n(n+1)}{2}\right)^2}$.
Exercice 8. Inspirez-vous des exercices 5 à 7 pour calculer $\sum_{k=1}^{n}k^4$.
Exercice 9. Consultez la page web « Formules de sommation et différences finies » à l'adresse :
www.fadagogo.com/histoires/html/diffin.html.
a) Utilisez la méthode des différences finies pour montrer que
$\sum_{k=0}^{n}k=\dfrac{n(n+1)}{2}$.
b) Utilisez la méthode des différences finies pour montrer que
$\sum_{k=0}^{n}k^3=\left(\dfrac{n(n+1)}{2}\right)^2$.
Exercices : séries géométriques
Les séries géométriques jouent aussi un grand rôle en mathématiques. Ce sont des expression de la forme :
$\sum_{k=0}^{n}ar^k$.
L'exercice suivant permet de conclure que si $r\ne1$, la valeur de cette somme est
$a\dfrac{1-r^{n+1}} {1-r}$.
(Pour $r=1$, la valeur de la somme est bien sûr $a(n+1)$.)
Exercice 10. a) Vérifiez que, pour tout nombre réel $x$ et pour tout nombre naturel $n$, on a
$(1+x+x^2+x^3+...+x^n)(1-x)=1-x^{n+1}$.
b) Déduisez de a) que pour tout nombre réel $x\neq1$,
${\sum_{i=0}^{n}x^i=\dfrac{1-x^{n+1}}{1-x}}$.
c) Calculer $\sum_{i=0}^{n}2^i$ et $\sum_{i=0}^{n}\dfrac{1}{2^i}$.
Beaucoup de légendes sont associées à la naissance du jeu d'échecs. Parmi celles-ci, plusieurs racontent l'histoire suivante : le souverain du royaume où le jeu fut inventé était tellement émerveillé qu'il offrit à l'inventeur du jeu la récompense de son choix. L'inventeur aurait demandé

au roi de lui donner un grain de riz (ou de blé, selon la version de la légende) pour la première case, deux grains pour la deuxième case, quatre grains pour la troisième case, huit pour la quatrième et ainsi de suite. Il est à noter qu'un échiquier comporte 64 cases (voir figure à droite).
Exercice 11. a) Combien de grains de riz le roi devra-t-il donner pour la 10ème case ?
b) Combien de grains de riz l'inventeur aura-t-il accumulé à la 20ème case ?
c) Quel est le nombre total des grains de riz que le roi doit remettre à l'inventeur ?
d) Si les faits se produisaient à l’époque actuelle, sachant qu’un grain de riz pèse en moyenne 0,02 g et que la production mondiale de riz est de 15200 kilos par seconde, quel serait le temps nécessaire pour récompenser l'inventeur ?
Raisonnements d'ordre géométrique
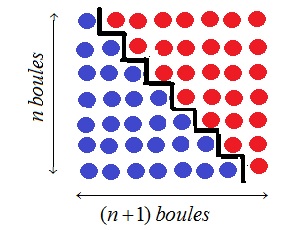
Certains résultats intéressants ont été obtenus par le mathématicien Al-Karaji (qui a vécu à Bagdad entre 953 et 1029) en utilisant des arguments d'ordre géométrique. Par exemple, si on considère les boules bleues dans l'empilement de $n(n+1)$ boules représenté à gauche, il devient évident qu'on doit avoir $\sum_{k=1}^{n}k=n(n+1)/2$.
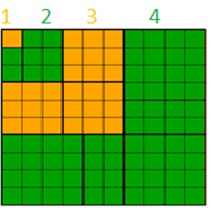
Al-Karaji a aussi utilisé une figure similaire à celle à droite pour montrer que
${\left( \sum_{k=1}^{n}k \right) }^2 = \sum_{k=1}^{n}k^3$
(voir l'exerice 9). Le raisonnement est basé sur le fait que
${\left( \sum_{i=1}^{k}i \right) }^2 = {\left( \sum_{i=1}^{k-1}i \right) }^2+k^3$.
(Pouvez-vous démontrer cette dernière formule ?)