Calcul des matrices de Jones
Nous montrons ici comment calculer les matrices de Jones pour un empilement de couches minces.
1. Matrices de Jones
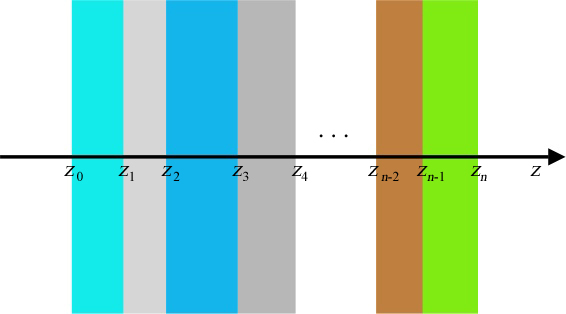
Supposons deux milieux homogènes isotropes et transparents séparés par $n$ couches minces pouvant être anisotropes, comme dans la figure de droite. Si dans le milieu entrant, à gauche, on a un champ incident $\boldsymbol\phi_{in}$, il en résultera dans le même milieu un champ réfléchi $\boldsymbol\phi_{re}$ et dans le milieu sortant, à droite, un champ transmis $\boldsymbol\phi_{tr}$. Les champs en $z=z_0$ et $z=z_n$ seront $$\begin{array} {ll} \boldsymbol\Phi(z_0) = \kk0+ \boldsymbol\phi_{in} + \kk0- \boldsymbol\phi_{re}, \\ \boldsymbol\Phi(z_n) = \kk{(n+1)}+ \boldsymbol\phi_{tr}. \end{array} \tag 1$$
Nous voulons trouver des matrices de Jones $\mat r_{0(n+1)}$ et $\mat t_{0(n+1)}$ telles que $$\begin{array} {ll} \boldsymbol\phi_{re} = \mat r_{0(n+1)} \boldsymbol\phi_{in}, & \boldsymbol\phi_{tr} = \mat t_{0(n+1)} \boldsymbol\phi_{in}. \end{array}$$ Le principe est le même que pour les coefficients de
Fresnel de la page précédente, mais il nous manque une donnée du problème : la matrice caractéristique $\mat N$ qui relie les b-vecteurs en $z=z_0$ et $z=z_n$ : $$\boldsymbol\Phi(z_0) = \mat N \boldsymbol\Phi(z_n).$$ Une fois cette matrice connue, on poura dire que $$\begin{split} \boldsymbol\Phi(z_0) & = \kk0+ \boldsymbol\phi_{in} + \kk0- \boldsymbol\phi_{re} \\ & = \mat N \kk{(n+1)}+ \boldsymbol\phi_{tr} \end{split} \tag 2$$ et en conclure, après multiplication à gauche de (2) par $\bb0+$ et $\bb0-$, que $$\begin{array} {ll} \phi_{in} = \bb0+ \mat N \kk{(n+1)}+ \boldsymbol\phi_{tr}, \\ \phi_{re} = \bb0- \mat N \kk{(n+1)}+ \boldsymbol\phi_{tr}. \end{array}$$ Les matrices qu'on cherche sont donc données par les formules $$\begin{array} {ll} \mat t_{0(n+1)} = [\bb0+ \mat N \kk{(n+1)}+]^{-1}, \\ \begin{split} \mat r_{0(n+1)} = & \bb0- \mat N \kk{(n+1)}+ \mat t_{0(n+1)} \\ = & \bb0- \mat N \kk{(n+1)}+ \times \\ & [\bb0+ \mat N \kk{(n+1)}+]^{-1}.\end{split} \end{array} \tag 3$$
2. Matrice caractéristique N
On a vu qu'il est possible, pour chacune des couches $k$, de calculer une matrice caractéristique $\mat N_k$ telle que $$\boldsymbol\Phi(z_{k-1}) = \mat N_k \boldsymbol\Phi(z_k).$$ On peut donc calculer $\mat N$ selon la formule $$\mat N = \mat N_1 \mat N_2 \cdots \mat N_{n-1} \mat N_n. \tag 4$$ Rappelons que pour calculer chaque matrice $\mat N_k$, il faut commencer par résoudre l'équation aux valeurs propres $$\boldsymbol\Delta_k |~k, i \gt = \zeta_{k,i} |~k, i \gt,$$ où $\boldsymbol\Delta_k$ la valeur de la matrice $\boldsymbol\Delta$ dans la couche $k$. On calcule ensuite la matrice $\mat M_k$ qui a les $|~k, i \gt$ comme colonnes ; $\mat N_k$ est alors donné par la formule
$$\mat N_k = \mat M_k \diag \left(e^{-i \frac \omega c \zeta_{k,1} d_k}, \ldots ,e^{-i \frac \omega c \zeta_{k,4} d_k}\right) \mat M_k^{-1},$$ où $$d_k = z_k-z_{k-1}$$ est l'épaisseur de la couche $k$. On peut aussi écrire $\mat N_k$ sous la forme équivalente $$\mkern -20mu \begin{split} \mat N_k & = \kk k+ \begin{bmatrix} e^{-i \frac \omega c \zeta_{k,1} d_k} & 0 \\ 0 & e^{-i \frac \omega c \zeta_{k,3} d_k} \end{bmatrix} \bb k+ \\ & +\kk k- \begin{bmatrix} e^{-i \frac \omega c \zeta_{k,2} d_k} & 0 \\ 0 & e^{-i \frac \omega c \zeta_{k,4} d_k} \end{bmatrix} \bb k-. \end{split} \tag 5$$
3. Champ incident venant de la droite
Si on répète le processus de la section 1 pour un champ incident venant de la droite, il faut remplacer (1) par $$\begin{array} {ll} \boldsymbol\Phi(z_0) = \kk0- \boldsymbol\phi_{tr}, & \boldsymbol\Phi(z_n) = \kk{(n+1)}- \boldsymbol\phi_{in} + \kk{(n+1)}+ \boldsymbol\phi_{re} \end{array}$$ et (2) par $$\boldsymbol\Phi(z_0) = \kk0- \boldsymbol\phi_{tr} = \mat N \kk{(n+1)}- \boldsymbol\phi_{in} + \mat N \kk{(n+1)}+ \boldsymbol\phi_{re}. \tag 6$$ En multipliant (6) à gauche par $\bb0+$ et $\bb0-$, on obtient $$\begin{array} {rr} 0 = \bb0+ \mat N \kk{(n+1)}- \boldsymbol\phi_{in} + \bb0+ \mat N \kk{(n+1)}+ \boldsymbol\phi_{re}, \\ \boldsymbol\phi_{tr} = \bb0- \mat N \kk{(n+1)}- \boldsymbol\phi_{in} + \bb0- \mat N \kk{(n+1)}+ \boldsymbol\phi_{re}. \end{array}$$ Si maintenant on définit les matrices de Jones $\mat r_{(n+1)0}$ et $\mat t_{(n+1)0}$ par $$\begin{array} {ll} \boldsymbol\phi_{re} = \mat r_{(n+1)0} \boldsymbol\phi_{in}, & \boldsymbol\phi_{tr} = \mat t_{(n+1)0} \boldsymbol\phi_{in}, \end{array}$$ ceci veut dire qu'on a $$\mat r_{(n+1)0} = - [ \bb0+ \mat N \kk{(n+1)}+ ]^{-1} \bb0+ \mat N \kk{(n+1)}- \tag {7a}$$ et $$\begin{split} \mat t_{(n+1)0} = & \bb0- \mat N \kk{(n+1)}- - \bb0- \mat N \kk{(n+1)}+ \times \\ & [ \bb0+ \mat N \kk{(n+1)}+ ]^{-1} \bb0+ \mat N \kk{(n+1)}-. \end{split} \tag {7b}$$
4. Autres formules
Dans le cas d'un champ incident venant de la droite, on peut simplifier les formules si on utilise $\mat N^{-1}$ plutôt que $\mat N$ : on peut en effet écrire $$\begin{split} \boldsymbol\Phi(z_n) & = \mat N^{-1} \kk0- \boldsymbol\phi_{tr} \\ & = \kk{(n+1)}- \boldsymbol\phi_{in} + \kk{(n+1)}+ \boldsymbol\phi_{re}, \end{split}$$ d'où $$\begin{array} {ll} \bb{(n+1)}+ \mat N^{-1} \kk0- \boldsymbol\phi_{tr} = \phi_{re} , \\ \bb{(n+1)}- \mat N^{-1} \kk0- \boldsymbol\phi_{tr} = \phi_{in} \end{array}$$ et $$\begin{array} {ll} \mat t_{(n+1)0} = [\bb{(n+1)}- \mat N^{-1} \kk0-]^{-1}, \\ \begin{split} \mat r_{(n+1)0} = & \bb{(n+1)}+ \mat N^{-1} \kk0- \mat t_{(n+1)0} \\ = & \bb{(n+1)}+ \mat N^{-1} \kk0- \times \\ & [\bb{(n+1)}- \mat N^{-1} \kk0-]^{-1}.\end{split} \end{array} \tag 8$$
Il est aussi possible, si on le désire, d'utiliser la matrice $\mat N^{-1}$ pour obtenir des formules similaires aux formules (7) lorsqu'on a un champ incident venant de la gauche.
Remarque. Lorsqu'on utilise la matrice $\mat N^{-1}$, on peut calculer la matrice $\mat N$ selon la formule (4), puis l'inverser numériquement. Une autre possibilité consiste à écrire $$\mat N^{-1} = \mat N_n^{-1} \mat N_{n-1}^{-1} \cdots \mat N_2^{-1} \mat N_1^{-1}, \tag 9$$ où $$\mkern -20mu \begin{split} \mat N_k^{-1} & = \mat M_k \diag \left(e^{i \frac \omega c \zeta_{k,1} d_k}, \ldots ,e^{i \frac \omega c \zeta_{k,4} d_k}\right) \mat M_k^{-1} \\ & =\kk k+ \begin{bmatrix} e^{i \frac \omega c \zeta_{k,1} d_k} & 0 \\ 0 & e^{i \frac \omega c \zeta_{k,3} d_k} \end{bmatrix} \bb k+ \\ & +\kk k- \begin{bmatrix} e^{i \frac \omega c \zeta_{k,2} d_k} & 0 \\ 0 & e^{i \frac \omega c \zeta_{k,4} d_k} \end{bmatrix} \bb k-. \end{split} \tag {10}$$
5. Miroir métallique en z = z0 ou en z = zn
Miroir métallique en z = z0
Comme on l'a vu, avoir un miroir métallique en $z=z_0$ est équivalent à supposer que le milieu $0$ est un conducteur parfait. On devra donc avoir $$\bb{}E \boldsymbol\Phi(z_0) = 0,$$ où la matrice $\bb{}E$, introduite à la page précédente, vaut $$\bb{}E = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}.$$
Avec un champ incident venant de la droite, on aura $$\boldsymbol\Phi(z_0) = \mat N \kk{(n+1)}- \boldsymbol\phi_{in} + \mat N \kk{(n+1)}+ \boldsymbol\phi_{re},$$ ce qui conduit à $$\begin{split} & \bb{}E \mat N \kk{(n+1)}- \boldsymbol\phi_{in} + \\ & \bb{}E \mat N \kk{(n+1)}+ \boldsymbol\phi_{re} = 0, \end{split}$$
et donc $$\begin{split} \mat r_{(n+1)0} = & [ \bb{}E \mat N \kk{(n+1)}+ ]^{-1} \times \\ & \bb{}E \mat N \kk{(n+1)}-.\end{split} \tag {11}$$
Miroir métallique en z = zn
Avec un miroir métallique en $z=z_n$ et un champ incident venant de la gauche, il est encore possible d'utiliser la matrice $\bb{}E$ si on inverse la matrice $\mat N$. On a alors $$\begin{split} & \bb{}E \mat N^{-1} \kk{0}+ \boldsymbol\phi_{in} + \\ & \bb{}E \mat N^{-1} \kk{0}- \boldsymbol\phi_{re} = 0 \end{split}$$ d'où $$\begin{split} \mat r_{0(n+1)} = & [ \bb{}E \mat N^{-1} \kk{0}- ]^{-1} \times \\ & \bb{}E \mat N^{-1} \kk{0}+.\end{split} \tag {12}$$
Une alternative faisant intervenir un autre type de matrice est présentée à la section 6.
6. Compléments, notes et références
Combinaison de deux empilements
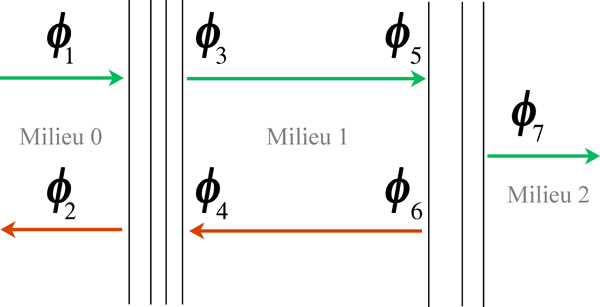
L'image à gauche illustre trois milieux ($0$, $1$ et $2$) séparés par deux empilements de couches minces. On suppose connues les différentes matrices de Jones entre les milieux $0$ et $1$ et entre les milieux $1$ et $2$ ; on veut calculer les matrices de Jones entre les milieux $0$ et $2$. Avec un champ incident $\boldsymbol\phi_1$ dans le milieu $0$, on aura un champ réfléchi $\boldsymbol\phi_2$ dans le même milieu et un champ transmis $\boldsymbol\phi_7$ dans le milieu $2$. Les relations entre les différents champs indiqués sur la figure seront : $$\begin{array} {llllll} \boldsymbol\phi_2 = \mat t_{10} \boldsymbol\phi_4 + \mat r_{01} \boldsymbol\phi_1, & \boldsymbol\phi_3 = \mat t_{01} \boldsymbol\phi_1 + \mat r_{10} \boldsymbol\phi_4, & \boldsymbol\phi_4 = \boldsymbol\pi_- \boldsymbol\phi_6, & \boldsymbol\phi_5 = \boldsymbol\pi_+ \boldsymbol\phi_3, & \boldsymbol\phi_6 = \mat r_{12} \boldsymbol\phi_5, & \boldsymbol\phi_7 = \mat t_{12} \boldsymbol\phi_5, \end{array}$$ où on a posé $$\begin{array} {ll} \boldsymbol\pi_+ = \begin{bmatrix} e^{i \frac \omega c \zeta_{1,1} d_1} & 0 \\ 0 & e^{i \frac \omega c \zeta_{1,3} d_1} \end{bmatrix}, & \boldsymbol\pi_- = \begin{bmatrix} e^{-i \frac \omega c \zeta_{1,2} d_1} & 0 \\ 0 & e^{-i \frac \omega c \zeta_{1,4} d_1} \end{bmatrix}, \end{array} \tag {13}$$ $d_1$ étant l'épaisseur du milieu $1$. On a ensuite successivement $$\begin{array} {ll} \boldsymbol\phi_6 = \mat r_{12} \boldsymbol\pi_+ \boldsymbol\phi_3, & \boldsymbol\phi_4 = \boldsymbol\pi_- \mat r_{12} \boldsymbol\pi_+ \boldsymbol\phi_3 \end{array}$$ et $$\boldsymbol\phi_3 = \mat t_{01} \boldsymbol\phi_1 + \mat r_{10} \boldsymbol\pi_- \mat r_{12} \boldsymbol\pi_+ \boldsymbol\phi_3~~\Rightarrow~~ \boldsymbol\phi_3 = [ \mat I - \mat r_{10} \boldsymbol\pi_- \mat r_{12} \boldsymbol\pi_+ ]^{-1}\mat t_{01} \boldsymbol\phi_1,$$ ce qui donne finalement $$\begin{array} {ll} \boldsymbol\phi_2 = \mat r_{01} \boldsymbol\phi_1 + \mat t_{10} \boldsymbol\pi_- \mat r_{12} \boldsymbol\pi_+ [ \mat I - \mat r_{10} \boldsymbol\pi_- \mat r_{12} \boldsymbol\pi_+ ]^{-1}\mat t_{01} \boldsymbol\phi_1, & \boldsymbol\phi_7 = \mat t_{12} \boldsymbol\pi_+ [ \mat I - \mat r_{10} \boldsymbol\pi_- \mat r_{12} \boldsymbol\pi_+ ]^{-1}\mat t_{01} \boldsymbol\phi_1. \end{array}$$ On a donc $$\begin{array} {ll} \mat r_{02} = \mat r_{01} + \mat t_{10} \boldsymbol\pi_- \mat r_{12} \boldsymbol\pi_+ [ \mat I - \mat r_{10} \boldsymbol\pi_- \mat r_{12} \boldsymbol\pi_+ ]^{-1}\mat t_{01}, & \mat t_{02} = \mat t_{12} \boldsymbol\pi_+ [ \mat I - \mat r_{10} \boldsymbol\pi_- \mat r_{12} \boldsymbol\pi_+ ]^{-1}\mat t_{01}. \end{array} \tag {14}$$
Remarque. Si le milieu $1$ est isotrope, alors $$\begin{array} {ll} \boldsymbol\pi_+=\boldsymbol\pi_-=e^{i \beta} \mat I, & \beta = \frac \omega c \zeta_1 d_1. \end{array} \tag {15}$$
Miroirs métalliques et matrice ∥ H ≫
En présence d'un miroir métallique, on peut aussi utiliser la matrice $$\kk{}H = \begin{bmatrix} 0 & 1 & 0 &0 \\ 0 & 0 & 0 & 1 \end{bmatrix}^T, \tag {16}$$ qui a la propriété $$\boldsymbol\phi_H = \begin{bmatrix} Z_0 H_y & Z_0 H_x \end{bmatrix}^T~~\Rightarrow~~\boldsymbol\Phi = \kk{}H \boldsymbol\phi_H = \begin{bmatrix} 0 & Z_0 H_y & 0 & Z_0 H_x \end{bmatrix}^T~: \tag {17}$$ quand on multiplie le pseudo j-vecteur $\boldsymbol\phi_H$ par $\kk{}H$, on obtient un b-vecteur $\boldsymbol\Phi$ qui satisfait la condition aux limites à la surface du miroir, $E_x=E_y=0$.
Supposons donc qu'on ait un miroir métallique en $z=z_n$ et un champ incident venant de la gauche : on aura, pour un certain pseudo j-vecteur $\boldsymbol\phi_H$, $$\begin{array} {ll} \boldsymbol\Phi(z_0) = \kk0+ \boldsymbol\phi_{in} + \kk0- \boldsymbol\phi_{re} , & \boldsymbol\Phi(z_n) = \kk{}H \boldsymbol\phi_H \end{array}$$ et donc $$\kk0+ \boldsymbol\phi_{in} + \kk0- \boldsymbol\phi_{re} = \mat N \kk{}H \boldsymbol\phi_H$$ En multipliant à gauche par $\bb0+$ et $\bb0-$, on obtient $$\begin{array} {ll} \phi_{in} = \bb0+ \mat N \kk{}H \boldsymbol\phi_H, & \phi_{re} = \bb0- \mat N \kk{}H \boldsymbol\phi_H \end{array},$$ ce qui implique que $$\mat r_{0(n+1)} = \bb0- \mat N \kk{}H [\bb0+ \mat N \kk{}H]^{-1}. \tag {18}$$