Les fonctions logiques de base sont au nombre de 4 : les fonctions OUI, NON, ET et OU. Les deux premières ont déjà été abordées dans le chapitre précédent, nous allons en faire un rapide résumé.
Chaque fonction logique va être abordée sous 4 angles : son schéma électrique, son équation, sa représentation sous forme d'ensembles et sa table de vérité.
1. la fonction "OUI"
La fonction OUI peut être matérialisée par un circuit électrique comportant un bouton poussoir travail
Son équation sera L = a puisque l'état électrique de L est identique à l'état physique de a.
L'ensemble les moments où L sera égal à 1 est confondu avec l'ensemble des moments où on actionne a.
La table de vérité montre que les états de L correspondent aux états de a.
| Schéma électrique | Équation | Ensembles | Table de vérité | ||||||
|---|---|---|---|---|---|---|---|---|---|
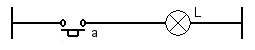 |
L = a | 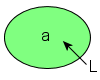 |
|
2. la fonction "NON"
La fonction NON peut être matérialisée par un circuit électrique comportant un bouton poussoir repos
Son équation sera L = b puisque l'état électrique de L est l'inverse de l'état physique de a.
L'ensemble les moments où L sera égal à 1 est extérieur à l'ensemble des moments où on actionne a.
La table de vérité montre que les états de L sont les inverses de ceux de a.
| Schéma électrique | Équation | Ensembles | Table de vérité | ||||||
|---|---|---|---|---|---|---|---|---|---|
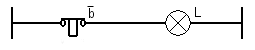 |
L = b | 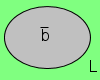 |
|
3. la fonction "ET" (and)
La fonction ET peut être matérialisée par un circuit électrique comportant deux boutons poussoirs travail mis à la suite l'un de l'autre, on dira qu'ils sont "en série".
Pour que la lampe L s'allume (état = 1), il faut pousser à la fois sur a ET sur b. L'ensemble les moments où L est égal à 1 est donc l'intersection des moments où on actionne a et des moments où on actionne b.
La table de vérité montre que l'état 1 de L n'est atteint que quand a ET b sont actionnés simultanément.
On peut se demander quelle fonction mathématique peut unir a et b pour obtenir les résultats de L. On voit rapidement que cette fonction est la multiplication. L'équation du ET sera donc L = a.b.
| Schéma électrique | Équation | Ensembles | Table de vérité | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
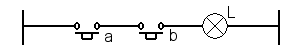 |
L = a.b | 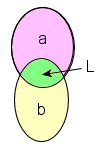 |
|
4. la fonction "OU" (or)
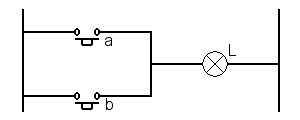
La fonction OU peut être matérialisée par un circuit électrique comportant deux boutons poussoirs travail mis "en parallèle" l'un par rapport à l'autre (voir schéma).
Pour que la lampe L s'allume (état = 1), il faut pousser sur a OU sur b. L'ensemble les moments où L est égal à 1 est donc la réunion des moments où on actionne a et des moments où on actionne b. On est en droit de se demander, quand on pousse simultanément sur a et sur b, si l'ampoule ne va pas exploser. Nous sommes en binaire, que le courant arrive à l'ampoule par un ou deux fils (ou un fil deux fois plus gros) ne change rien, c'est toujours le même courant.
La table de vérité montre que l'état 1 de L est atteint dès qu'on actionne a OU qu'on actionne b, que ce soit simultanément ou pas.
On peut se demander quelle fonction mathématique peut unir a et b pour obtenir les résultats de L. On voit rapidement que cette fonction est l'addition. L'équation du OU sera donc L = a + b.
| Schéma électrique | Équation | Ensembles | Table de vérité | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
L = a + b | 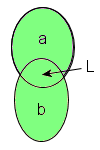 |
|
Grâce à la connaissance des circuits électriques et à ces fonctions logiques, nous allons pouvoir examiner les propriétés principales de l'algèbre de Boole. Ce sera le sujet du chapitre suivant.