En électricité, il faut toujours deux fils : un fil par lequel le courant électrique arrive et l'autre par lequel il repart. Pour que le circuit fonctionne, il ne faut pas qu'il y ait d'interruption sur aucun des deux fils, on dit que le circuit doit être fermé. S'il y a une interruption, le circuit est ouvert, le courant ne passe pas.
Prenons le cas simple d'une ampoule électrique et simplifions à l'extrême les éléments minimums dont est constitué le circuit électrique de cette ampoule. Attention : il vous est strictement interdit de réaliser ce branchement en réalité, cela pourrait entraîner la mort par électrocution d'une ou plusieurs personnes.
Si l'ampoule est celle d'une lampe de poche, son circuit devient plus simple (et, celui-là, vous pouvez le réaliser en toute sécurité), il va ressembler à ceci :

Pour nous faciliter la tâche, nous allons réduire ce circuit à sa plus simple expression en faisant abstraction de la source de courant et en stylisant l'interrupteur et l'ampoule. Les circuits que nous utiliserons à l'avenir seront du type suivant
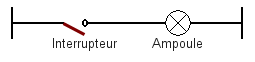
Nous voyons que ces circuits vont se composer essentiellement de fils, de récepteurs comme l'ampoule et d'effecteurs comme l'interrupteur.
A. Les récepteurs
Les récepteurs vont être les ampoules, les moteurs, les relais (abordés plus tard dans les fonctions mémoires),... Ils seront toujours représentés par des lettres majuscules.
Quand ils reçoivent du courant (1), ils fonctionnent (1), quand ils ne reçoivent pas de courant (0), ils ne fonctionnent pas (0). L'état du récepteur 1 ou 0 est donc son état électrique, courant 1 ou pas courant 0. Tout ça est donc très simple.
B. Les effecteurs
Les effecteurs sont essentiellement les interrupteurs, les éléments qu'on doit manipuler pour que le courant passe ou ne passe pas. Ils seront toujours représentés par des lettres minuscules
Les interrupteurs conventionnels, comme ceux qu'il y a dans votre maison, ne conviennent pas car ils restent dans leur dernier état jusqu'à la prochaine manipulation. Ce que nous cherchons, ce sont des interrupteurs qui, lorsqu'on ne pousse plus dessus, reviennent à leur état de base. Ces interrupteurs s'appellent des boutons poussoirs et c'est exclusivement ceux-là que nous allons utiliser.
Il va y avoir deux types de boutons poussoirs : les boutons poussoirs travail et les boutons poussoirs repos. Dans les 2 cas, il faut considérer qu'on pousse ces boutons poussoirs vers le haut et que, quand on les relâche, ils redescendent instantanément à leurs positions d'origine. L'état de l'effecteur 1 ou 0 est donc son état physique, on pousse dessus 1 ou on ne pousse pas dessus 0. Tout ça est donc très simple.

1. Le bouton poussoir "travail"
Voici un schéma électrique simplifié possédant un bouton poussoir travail
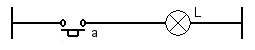
Avec ce schéma, nous pouvons nous poser la question de savoir quel est l'état électrique de l'ampoule L en fonction de l'état physique du bouton poussoir a
- dans l'état actuel du schéma, l'état électrique de L = 0 du fait que l'état physique de a = 0;
- si on pousse sur le bouton a, l'état électrique de L = 1 du fait que l'état physique de a = 1;
Ceci nous permet d'établir notre première équation logique valable pour le bouton poussoir travail
L = a; ce qui veut dire que, dans le cas d'un bouton poussoir travail, l'état électrique du récepteur est égal à l'état physique de l'effecteur.
Voici un tableau récapitulatif
| Schéma électrique | État physique de a | État électrique de L |
|---|---|---|
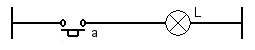 | 0 | 0 |
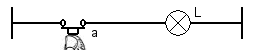 | 1 | 1 |
2. Le bouton poussoir "repos"
Voici un schéma électrique simplifié possédant un bouton poussoir repos
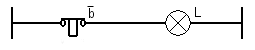
Avec ce schéma, nous pouvons nous poser la question de savoir quel est l'état électrique de l'ampoule L en fonction de l'état physique du bouton poussoir b
- dans l'état actuel du schéma, l'état électrique de L = 1 du fait que l'état physique de b = 0;
- si on pousse sur le bouton b, l'état électrique de L = 0 du fait que l'état physique de b = 1;
Ceci nous permet d'établir notre seconde équation logique valable pour le bouton poussoir repos :
L = non b; ce qui veut dire que, dans le cas d'un bouton poussoir repos, l'état électrique du récepteur est l'inverse de l'état physique de l'effecteur.
Pour une notation plus simplifiée encore, nous allons "compacter" ce terme "non b" en l'écrivant b, ce qui se prononce "b barre". L'équation deviendra donc L = b, qui se dit "L = b barre".
Voici un tableau récapitulatif
| Schéma électrique | État physique de b | État électrique de L |
|---|---|---|
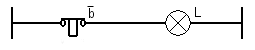 | 0 | 1 |
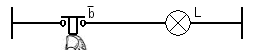 | 1 | 0 |
C. Les circuits
Les circuits peuvent prendre des formes variées avec de nombreux effecteurs et récepteurs. En voici un exemple
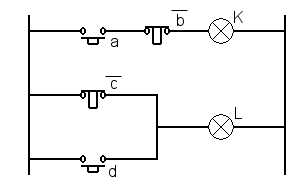
Ceci nous permettra d'illustrer les fonctions logiques de base, matière du prochain chapitre.