Maurice Karnaugh est né à New-York le 4 octobre 1924. Expert logicien, il met au point sa table de simplification en 1953 lorsqu'il travaille aux célèbres laboratoires Bell (USA).
Son tableau de simplification "automatique" est largement utilisé dans le monde de la logique. Voyons sans plus attendre en quoi il consiste.
Admettons que j'aie un mélange de pièces qui soient des petits et grands carrés et des petits et grands ronds. Comment les classer ?
J'ai 4 sortes de pièces différentes, je vais donc prendre une boîte à 4 compartiments afin de classer les pièces de la façon suivante, par exemple.
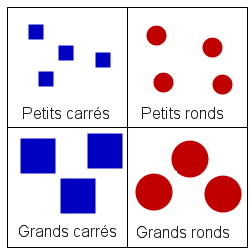
Symboliquement, je peux représenter ce tri dans un tableau à 2 dimensions, la dimension verticale étant la forme et la dimension horizontale étant la taille.
| Pièces (P) | Forme | ||
|---|---|---|---|
| Carrés | Ronds | ||
| Taille | Petits | Petits carrés | Petits ronds |
| Grands | Grands carrés | Grandes ronds | |
Étant donné la particularité des pièces en présence, je peux utiliser la notation de Boole pour rationaliser l'appellation des pièces
- Je nomme la caractéristique "ronde" par r et, la caractéristique "carrée" (non ronde), par r
- Je nomme la caractéristique "grande" par g et, la caractéristique "petite" (non grande), par g
| P | r | r |
|---|---|---|
| g | 1 g.r | 2 g.r |
| g | 3 g.r | 4 g.r |
dans lequel le "." représente la multiplication, c'est-à-dire la fonction ET. Les cases contiennent donc
- La case 1 : les pièces g.r, c'est-à-dire les pièces petites ET carrées;
- La case 2 : les pièces g.r, c'est-à-dire les pièces petites ET rondes;
- La case 3 : les pièces g.r, c'est-à-dire les pièces grandes ET carrées;
- La case 4 : les pièces g.r, c'est-à-dire les pièces grandes ET rondes;
Sachant qu'en algèbre de Boole, on peut remplacer les lettres par 1 et leurs contraires (lettres barrées) par 0, le tableau peut prendre sa forme finale
| P | r | ||
|---|---|---|---|
| 0 | 1 | ||
| g | 0 | g r | g r |
| 1 | g r | g r | |
où on retrouve les mêmes pièces dans les mêmes cases.
Reste maintenant à voir pourquoi la simplification grâce à ce tableau est si géniale et facile. Ce sera le sujet du chapitre suivant.