Au chapitre précédent nous avons vu comment organiser les différentes pièces dans un tableau de Karnaugh en fonction de leurs formes et de leurs tailles. L'objectif de ce chapitre est de savoir : lorsque certaines pièces manquent, par quelle expression booléenne minimum puis-je représenter l'ensemble des pièces présentes ou absentes.
Un petit exercice va nous permettre de comprendre cela plus facilement. Imaginons, dans la caisse du chapitre précédent, que je ne dispose que de grands carrés et de grands ronds.
L'équation des pièces présentes sera P = g.r + g.r. Y a-t-il moyen de simplifier cette équation logique autrement que de façon algébrique ? Oui, la marche à suivre sera la suivante :
1. Je vais reporter dans le tableau de Karnaugh les 0 correspondant aux cases vides et les 1 correspondant aux cases pleines. J'obtiendrai le tableau suivant :
| P | r | ||
|---|---|---|---|
| 0 | 1 | ||
| g | 0 | 0 | 0 |
| 1 | 1 | 1 | |
2. Il faut maintenant regrouper toutes les cases qui contiennent la valeur 1 (les pièces présentes) par un ensemble (jaune ici) :
| P | r | ||
|---|---|---|---|
| 0 | 1 | ||
| g | 0 | 0 | 0 |
| 1 | 1 | 1 | |
3. Je constate que l'ensemble jaune correspond à la ligne g = 1. L'équation des pièces présentes devient P = g, ce qui veut dire que les pièces présentes sont uniquement les grandes.
Par la simplification classique, nous aurions dû passer par les étapes suivantes :
- L'équation des pièces présentes est P = g.r + g.r;
- Par une mise en évidence, nous pouvons obtenir P = g.(r + r);
- Or, un élément + son contraire est égal à 1 : P = g.(1);
- Ce qui se simplifie en P = g.
La méthode de simplification par les tableaux de Karnaugh sera d'autant plus efficace que les cas abordés seront compliqués.
Si je m'intéresse aux pièces absentes, que je peux regrouper grâce à l'ensemble rose, je vois que l'équation est P = g : les pièces absentes sont les petites.
Prenons un autre exemple un peu plus substantiel.
À travers cet exemple plus important, nous allons voir quelles sont les règles précises à mettre en œuvre pour effectuer des simplifications grâce au tableau de Karnaugh.
Exemple : dans les rayons d'un magasin, nous avons un ensemble de boîtes de conserve de légumes (voir schéma ci-dessous) :
- des petites et des grandes;
- celles contenant des haricots et celles contenant des carottes;
- des boîtes rectangulaires et des boîtes ovales.
Étape 1
La première étape est d'assigner des lettres aux différentes catégories de boîtes. Nous pouvons, par exemple, prendre la convention suivante :
- la lettre g pour la taille des boîtes : les grandes = g et les non grandes = g;
- la lettre c pour le contenu des boîtes : les carottes = c et les non carottes (ici les haricots) = c;
- la lettre v pour la forme des boîtes : les ovales = v (pas la lettre o pour ne pas la confondre avec le 0 zéro) et les non ovales (ici les rectangulaires) = v;
- reste à définir la lettre qui correspondra à l'ensemble des boîtes : B pour Boîtes (B est majuscule puisque l'ensemble des boîtes est le résultat de la présence des boîtes ayant les caractéristiques ci-dessus).
Étape 2
Lorsqu'il y a deux lettres dans une dimension, l'ordre des 0 et des 1 doit répondre à une succession précise (appelée code de Gray). D'une colonne à l'autre, il ne peut y avoir qu'une seule valeur qui change à la fois. La succession suivante :
- 00 → 01 ↝ 10 → 11 et retour ↝ 00 n'est pas correcte car les 2 valeurs changent 2 fois (flèches ↝);
- 00 → 01 → 11 → 10 et retour → 00 est correcte car 1 seule des valeurs change à chaque fois.
Le tableau de Karnaugh sera donc celui-ci :
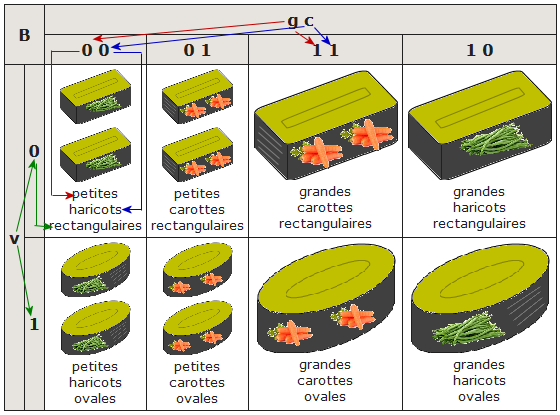
De façon plus succincte :
| B | g c | ||||
|---|---|---|---|---|---|
| 0 0 | 0 1 | 1 1 | 1 0 | ||
| v | 0 | g c v | g c v | g c v | g c v |
| 1 | g c v | g c v | g c v | g c v | |
Tableau dans lequel nous pouvons repérer différentes "plages" : les petites boîtes (jaune), les grandes (bleue). Pouvez-vous repérer la constante dans chacune de ces plages (*a) ? Si nécessaire, reportez-vous aux dessins ci-dessus.
| B | g c | ||||
|---|---|---|---|---|---|
| 0 0 | 0 1 | 1 1 | 1 0 | ||
| v | 0 | g c v | g c v | g c v | g c v |
| 1 | g c v | g c v | g c v | g c v | |
Les haricots (vert) et les carottes (rouge). Pouvez-vous repérer la constante dans chacune de ces plages (*b) ?
| B | g c | ||||
|---|---|---|---|---|---|
| 0 0 | 0 1 | 1 1 | 1 0 | ||
| v | 0 | g c v | g c v | g c v | g c v |
| 1 | g c v | g c v | g c v | g c v | |
Les boîtes rectangulaires (orange) et les ovales (gris). Pouvez-vous repérer la constante dans chacune de ces plages (*c) ?
| B | g c | ||||
|---|---|---|---|---|---|
| 0 0 | 0 1 | 1 1 | 1 0 | ||
| v | 0 | g c v | g c v | g c v | g c v |
| 1 | g c v | g c v | g c v | g c v | |
* Réponses :
- a : l'ensemble jaune est celui des petites boîtes g, l'ensemble bleu celui des grosses boîtes g;
- b : l'ensemble vert est celui des haricots c, l'ensemble rouge est celui des carottes c;
- c : l'ensemble orange est celui des boîtes rectangulaires v, l'ensemble gris est celui des boîtes ovales v.
Nous visitons le magasin et remarquons les boîtes présentes dans les rayons :
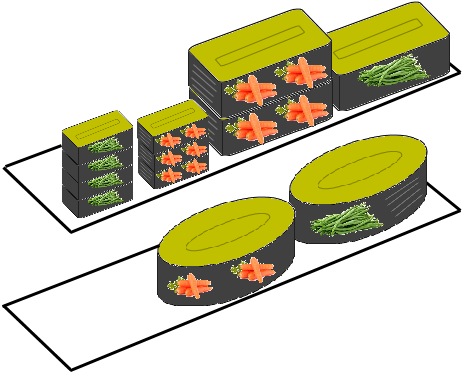
Étape 3
Reportons dans le tableau de Karnaugh les 1 et les 0 dans les cases en fonction de la présence ou de l'absence des boîtes correspondantes. Nous obtenons ceci :
| B | g c | ||||
|---|---|---|---|---|---|
| 0 0 | 0 1 | 1 1 | 1 0 | ||
| v | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | |
Étape 4
Intéressons-nous maintenant aux boîtes présentes, nous allons donc grouper les 1. Il faut réaliser les groupements les plus grands, même s'ils se superposent, par puissances de 2 (pour rappel, nous sommes en binaire).
Les cases groupées le seront donc, si possible, soit par 24 (16), 23 (8), 22 (4), 21 (2) ou 20 (1).
Dans notre cas, nous pouvons faire 2 groupements de 4 : le groupement jaune et le groupement orange (qui doivent normalement se faire dans le même tableau, mais que nous séparons pour la visibilité).
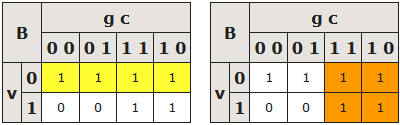
Étape 5
Il ne reste plus qu'à caractériser les groupements (voir à quelle(s) lettre(s) ils correspondent). Pour les boîtes présentes :
- le groupement jaune de gauche correspond à v;
- le groupement orange de droite correspond à g.
Pour les boîtes absentes, le groupement aura été fait sur les 0 (groupement rose) :
| B | g c | ||||
|---|---|---|---|---|---|
| 0 0 | 0 1 | 1 1 | 1 0 | ||
| v | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | |
Il faut maintenant trouver les lettres qui sont constantes dans tout ce groupement. Nous voyons qu'il s'agit de l'intersection des lignes et colonnes correspondant aux lettres v ET g. L'équation des boîtes absentes devient donc B = v g. En français : "Il manque les boîtes ovales et petites", ce qui est exact.
Profitons pour observer une règle générale à tous les groupements :
- Si on groupe la moitié des cases d'un tableau, ce groupement sera représenté par 1 lettre;
- Si on groupe le quart des cases d'un tableau, ce groupement sera représenté par 2 lettres;
- Si on groupe le huitième des cases d'un tableau, ce groupement sera représenté par 3 lettres...
Par exemple, nous savons déjà que la case inférieure droite du tableau représente un huitième des cases de ce tableau et qu'elle est identifiée par les 3 lettres g c v (grandes boîtes de haricots ovales).
La théorie de ce chapitre est terminée, voici un bref rappel des règles pour effectuer des simplifications grâce au tableau de Karnaugh, règles qui vous serviront dans les exercices du chapitre suivant.
Étapes :
- Attribuez des lettres aux différents éléments en présence en fonction de leurs caractéristiques;
- Construisez un tableau de Karnaugh adapté au nombre de lettres en respectant le code de Gray;
- Placez dans les cases un 1 si l'élément est présent, un 0 s'il est absent;
- Effectuez les groupements maximum par puissances de 2 (16, 8, 4, 2, 1) sachant que les tableaux sont sphériques (le bord droit rejoint le gauche et le bas rejoint le haut);
- Déterminez les lettres communes à chaque groupement et additionnez-les dans l'équation finale...
... ce qui ne reste plus qu'à appliquer. Bons exercices.