Les différentes identités trigonométriques sont connues depuis longtemps et ont été initialement obtenues avec des raisonnements élémentaires de géométrie plane.
Le théorème de la corde brisée, démontré par Archimède, dit que si l’arc $ABC$ est bissecté par le point $M$, et si $F$ est le pied de la perpendiculaire abaissée de $M$ sur $BC$ (la plus longue des deux cordes formant la corde brisée $ABC)$, alors $F$ bissecte la corde brisée, autrement dit $\overline{AB}+\overline{BF}=\overline{FC}$.
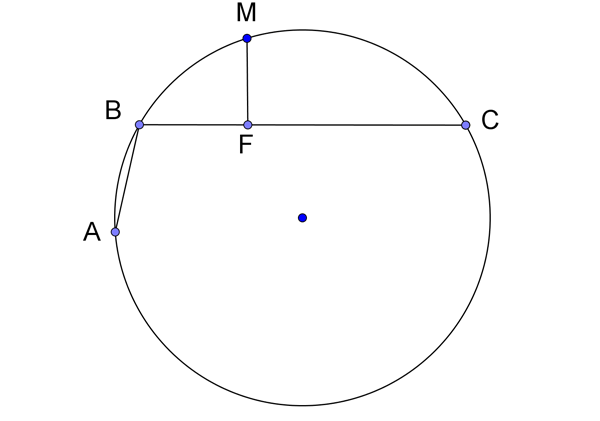
Nous allons démontrer le théorème de la corde brisée et l’utiliser pour démontrer les identités trigonométriques $$\sin(x - y) = \sin x \cos y - \sin y \cos x$$ et $$\sin(x + y) = \sin x \cos y + \sin y \cos x.$$ Les préalables pour comprendre ces démonstrations sont des résultats très élémentaires de géométrie plane.
Document compagnon : Vous trouverez ici un document qui revient sur quelques concepts vus dans la vidéo.