Polarisation dans les milieux anisotropes
Nous continuons ici l'étude des milieux anisotropes infinis commencée à la page précédente. Nous continuerons à nous limiter au cas où le tenseur de permittivité diélectrique relative $\eps'$ est réel.
1. Tenseur de permittivité diélectrique relative inverse et ellipsoïde des indices
Introduisons le tenseur de permittivité diélectrique relative inverse $\boldsymbol{\eta'}$ défini par $$\boldsymbol{\eta'}\boldsymbol{\eps'} = \boldsymbol{\eps'}\boldsymbol{\eta'} = \vec{I}.$$ Dans un système d'axes où $\boldsymbol{\eps'}$ est diagonal, $\boldsymbol{\eta'}$ sera de la forme $$\boldsymbol{\eta'} = \begin{bmatrix} \eta'_1 & 0 & 0 \\ 0 & \eta'_2 & 0 \\ 0 & 0 & \eta'_3 \end{bmatrix} = \begin{bmatrix} 1/\eps'_1 & 0 & 0 \\ 0 & 1/\eps'_2 & 0 \\ 0 & 0 & 1/\eps'_3 \end{bmatrix}.$$ Dans les autres systèmes d'axes orthonormés, $\boldsymbol{\eta'}$ sera un tenseur symétrique. On vérifie que la surface d'équation $$\vec{x} \cdot \boldsymbol{\eta'} \vec{x} = 1$$
est un ellipsoïde, qui porte le nom d'ellipsoïde des indices.
Pour étudier la polarisation, on utilisera non pas le champ électrique $\fvec{E}$, mais plutôt le déplacement électrique $\fvec{D}$, qu'on écrira sous la forme $$\fvec{D}(\vec{x})=\eps_0 \exp(i\vec{k} \cdot \vec{x})~\vec{d}.$$ Le vecteur $\vec{d}$ est relié au vecteur $\vec{e}$ de la page précédente par $$\vec{d}=\boldsymbol{\eps'}\vec{e}~~\Rightarrow~~\vec{e}=\boldsymbol{\eta'}\vec{d}.$$ Notons qu'il résulte de l'équation (1) de cette même page qu'on doit avoir $$\boldsymbol{\ka} \cdot \vec{d}=0.$$
2. Ondes planes : polarisation
Pour étudier la polarisation des ondes planes, le plus simple est de se situer dans un repère où le vecteur d'onde réduit $\boldsymbol{\ka}$ est parallèle à l'axe des $z$ : $$\boldsymbol{\ka}= \ka \uvec{z}.$$ On a alors $d_z =0$ : le vecteur $\vec{d}$ doit donc être situé dans le plan $xy$. L'équation (1) de la page précédente peut être réécrite sous la forme équivalente $$ \boldsymbol{\eta'} \vec{d} - \uvec{z} (\uvec{z} \cdot \boldsymbol{\eta'} \vec{d}) = \dfrac{1}{\ka^2} \vec{d}$$ et on constate qu'elle se réduit en fait à une équation à deux dimensions : $$\begin{bmatrix} \eta'_{xx} & \eta'_{xy} \\ \eta'_{yx} & \eta'_{yy} \end{bmatrix} \begin{bmatrix} d_x \\ d_y \end{bmatrix} = \dfrac{1}{\ka^2} \begin{bmatrix} d_x \\ d_y \end{bmatrix}$$ jointe à la condition déjà mentionnée $d_z =0$.
La conclusion, c'est que le vecteur $[d_x~d_y]^T$ doit être un
vecteur propre de la matrice $$\begin{bmatrix} \eta'_{xx} & \eta'_{xy} \\ \eta'_{yx} & \eta'_{yy} \end{bmatrix} \tag{1}$$ et que la valeur propre correspondante $\lambda$ doit être reliée à l'indice de réfraction équivalent $\ka$ par la relation $$\lambda = \dfrac{1}{\ka^2}.$$ Comme la matrice (1) est une matrice réelle symétrique, ses valeurs propres $\lambda$ sont réelles et ses vecteurs propres (dans le cas non dégénéré) sont pependiculalres. Dans le cas général, les deux états de polarisation possibles du déplacement électrique sont donc des états de polarisation linéaire dans deux directions perpendiculaires.
Dans le cas où $\boldsymbol{\ka}$ est parallèle à un des axes optiques, par contre, la matrice (1) est un multiple de l'identité et toutes les polarisations deviennent alors possibles, y compris les polarisations elliptiques ou circulaires.
3. Interprétation géométrique
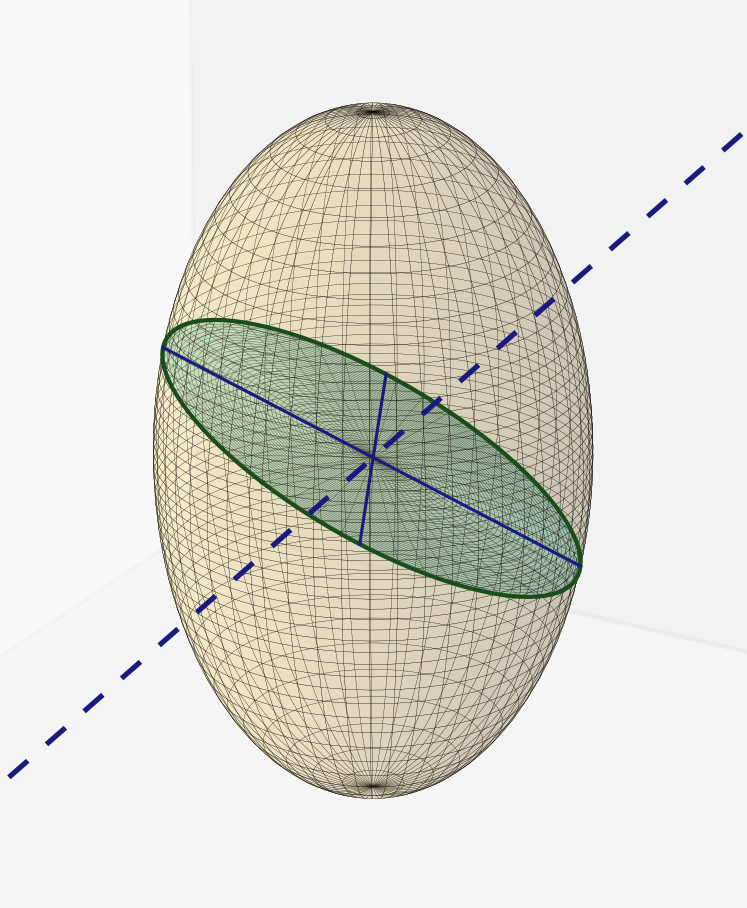
Le problème de la section précédente admet une interprétation géométrique. En effet, l'équation $$\begin{bmatrix} x & y \end{bmatrix} \begin{bmatrix} \eta'_{xx} & \eta'_{xy} \\ \eta'_{yx} & \eta'_{yy} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = 1$$ est l'équation d'une ellipse qui est l'intersection de l'ellipsoïde des indices avec le plan $xy$. La direction des axes de cette ellipse correspond avec la direction des vecteurs propres de (1) et donc des polarisations possibles de $\fvec{D}$ ; de plus, les longueurs des axes de l'ellipse coïncident avec les valeurs correspondantes de $\ka$.
Cette interprétation est indépendante de l'orientation de l'ellipsoïde et de la direction de propagation. Dans le cas général, il suffit de remplacer le plan $xy$ par le plan perpendiculaire à $\boldsymbol{\ka}$ qui passe par le centre de l'ellipsoïde. La figure à droite illustre la situation pour un cristal uniaxe : une direction de propagation (en pointillé) et les directions de polarisation correspondantes sont indiquées en bleu.
4. Notes et références
Il est facile de voir sur la figure de la section 3 que si la direction de propagation était verticale, l'ellipse en vert serait en fait un cercle. Géométriquement, c'est ce qui signale la dégénérescence de la valeur propre pour une propagation parallèlement à un axe optique¹.
On peut aussi, à partir de cette figure, tirer d'autres conclusions concernant les cristaux uniaxes :
- Pour une direction de propagation donnée, une des directions de polarisation est située dans le plan Π contenant la direction de propagation et l'axe optique ;
- L'autre direction de polarisation est perpendiculaire au plan Π et son indice de réfraction équivalent est le même que pour la propagation parallèlement à l'axe optique (on l'appelle l'indice ordinaire du cristal, l'indice effectif pour l'autre direction de polarisation étant dit extraordinaire).
Les désultats de cette page sont difficiles à exploiter lorsqu'il y a une interface avec un autre milieu : en effet, la polarisation calculée ici l'est pour le déplacement électrique, alors que ce sont les composantes tangentielles du champ électrique qui sont conservées à l'interface.
¹ Ceci est aussi valide pour les cristaux biaxes, mais serait plus difficile à illustrer et à visualiser (c'est ce qui a motivé notre choix d'un cristal uniaxe pour la figure).