Propagation dans les milieux anisotropes
Nous voulons voir ici sous quelles conditions la lumière peut se propager dans un milieu anisotrope infini.
1. Tenseur de permittivité diélectrique

gauche est isotrope, celui de droite est anisotrope.
Les milieux anisotropes sont des milieux cristallins où, à cause de la structure du matériau, la polarisation n'est généralement pas parallèle au champ électrique. Si le milieu est linéaire, on aura alors entre les champ et déplacement électriques une relation où la permittivité diélectrique est un tenseur : $$\begin{array} {lll} \fvec{D} = \boldsymbol{\eps} \fvec{E}, & \boldsymbol{\eps}=\eps_0 \boldsymbol{\eps'}, & \boldsymbol{\eps'} = \begin{bmatrix} \eps'_{xx} & \eps'_{xy} & \eps'_{xz} \\ \eps'_{yx} & \eps'_{yy} & \eps'_{yz} \\ \eps'_{zx} & \eps'_{zy} & \eps'_{zz} \end{bmatrix}. \end{array}$$
Symétrie du tenseur ε'
Comme la majorité des auteurs qui traitent de l'optique des milieux anisotropes, nous nous limiterons au cas où le tenseur de permittivité diélectrique relative $\boldsymbol{\eps'}$ est réel. On peut alors montrer que ce tenseur doit être symétrique : $$\begin{array} {lll}\eps'_{yx}=\eps'_{xy}, & \eps'_{zx}=\eps'_{xz}, & \eps'_{zy}=\eps'_{yz}. \end{array}$$
Ceci implique qu'il existe un système d'axes où $\boldsymbol{\eps'}$ est diagonal : $$\boldsymbol{\eps'} = \begin{bmatrix} \eps'_1 & 0 & 0 \\ 0 & \eps'_2 & 0 \\ 0 & 0 & \eps'_3 \end{bmatrix}.$$
Classification des milieux anisotropes
Plusieurs cas peuvent se présenter :- Le cas le plus simple est évidemment celui où
- $\eps'_1= \eps'_2 = \eps'_3,$ mais dans ce cas il n'y a rien a dire, car le milieu est tout simplement isotrope.
- Les milieux anisotropes les plus faciles à traiter (et de loin) sont ceux pour lesquels deux des éléments diagonaux sont égaux :$$\eps'_1= \eps'_2 \ne \eps'_3.$$ On les appelle des milieux uniaxes (on verra la raison de cette appellation un peu plus loin). Si $\eps'_3$ est la plus grande des trois valeurs, on dit qu'on a un milieu uniaxe positif. Dans le cas contraire, on dit que le milieu uniaxe est négatif.
- Dans le cas où $\eps'_1$, $\eps'_2$ et $\eps'_3$ sont tous les trois différents, on dit qu'on est dans un milieu anisotrope biaxe (on verra plus loin pourquoi). Il est d'usage de supposer que les axes sont choisis de telle manière que $$\eps'_1 \lt \eps'_2 \lt \eps'_3.$$
2. Ondes planes : existence
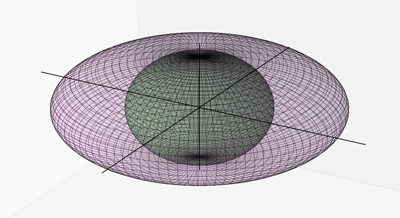
un cristal uniaxe positif.
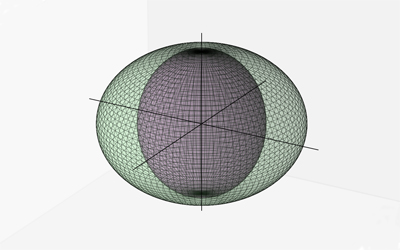
un cristal uniaxe négatif.
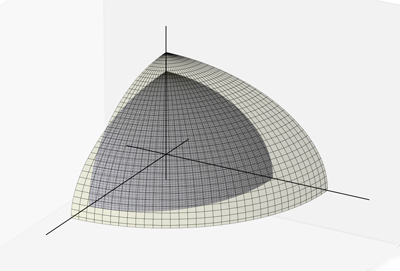
un cristal biaxe. On a seulement représenté
un huitième de la surface pour ne pas obscur-
cir les détails.
Voyons maintenant quels types d'ondes planes peuvent se propager dans un milieu anisotrope donné. En partant des équations de Maxwell-Lorentz libres $$\begin{array} {ll} \nabla \times \fvec{H} + i\omega \boldsymbol{\eps} \fvec{E} = 0, & \nabla \times \fvec{E}-i \omega \fvec{B} =0. \end{array}$$ et en effectuant les mêmes démarches qu'à la page précédente, avec les mêmes notations, on est conduit à l'équation $$\boldsymbol{\ka} \times (\boldsymbol{\ka} \times \vec{e}) + \boldsymbol{\eps'} \vec{e} = \boldsymbol{\ka} (\boldsymbol{\ka} \cdot \vec{e}) - \ka^2 \vec{e} + \boldsymbol{\eps'} \vec{e} = 0. \tag{1}$$Dans un système d'axes où $\boldsymbol{\eps'}$ est diagonal, ce système d'équations linéaires homogène prend la forme $$\begin{bmatrix} \eps'_1-\ka_y^2-\ka_z^2 & \ka_x\ka_ y& \ka_x\ka_z \\ \ka_y\ka_x & \eps'_2-\ka_x^2-\ka_z^2 & \ka_y\ka_z \\ \ka_z\ka_x & \ka_z\ka_y & \eps'_3-\ka_x^2-\ka_y^2 \end{bmatrix} \begin{bmatrix} e_x \\ e_y \\ e_z \end{bmatrix} = 0 \tag{2}.$$ Il a une solution si et seulement si le déterminant $$\Delta(\boldsymbol{\ka}) = \begin{vmatrix} \eps'_1-\ka_y^2-\ka_z^2 & \ka_x\ka_ y& \ka_x\ka_z \\ \ka_y\ka_x & \eps'_2-\ka_x^2-\ka_z^2 & \ka_y\ka_z \\ \ka_z\ka_x & \ka_z\ka_y & \eps'_3-\ka_x^2-\ka_y^2 \end{vmatrix}$$ est nul. On peut vérifier qu'on a $$\begin{split} \Delta(\boldsymbol{\ka}) = & \ka^2 (\eps'_1\ka_x^2+\eps'_2\ka_y^2+\eps'_3\ka_z^2) -[\eps'_1\eps'_2(\ka_x^2+\ka_y^2)+ \\ & \eps'_1\eps'_3(\ka_x^2+\ka_z^2)+\eps'_2\eps'_3(\ka_y^2+\ka_z^2)]+\eps'_1\eps'_2\eps'_3 \end{split} $$ ou encore, en posant $\boldsymbol{\ka} = \ka \uvec{u}$, $$\begin{split} \Delta(\boldsymbol{\ka}) = & \ka^4 (\eps'_1u_x^2+\eps'_2u_y^2+\eps'_3u_z^2) - \ka^2 [\eps'_1\eps'_2(u_x^2+u_y^2)+ \\ & \eps'_1\eps'_3(u_x^2+u_z^2)+\eps'_2\eps'_3(u_y^2+u_z^2)]+\eps'_1\eps'_2\eps'_3. \end{split} $$
On peut alors calculer les valeurs possibles de $\ka$ pour chaque direction donnée par le vecteur unitaire $\uvec{u}$, ce qui a permis de dessiner les trois figures à droite¹.
¹ Les paramètres utilisés pour dessiner ces figures ne sont pas des plus réalistes. Ils ont été choisis pour mieux mettre en évidence les caractéristiques des surfaces.
3. Remarques sur la surface Δ(κ)=0 – Axes optiques
L'équation $\Delta(\boldsymbol{\ka})=0$ est biquadratique en $\ka$, mais étant donné sa symétrie, la surface $\Delta(\boldsymbol{\ka})=0$ est constituée de seulement deux feuillets, comme on peut le constater sur les figures.
Cette surface a une interprétation physique : la dépendance spatio-temporelle des ondes planes de vecteur d'onde réduit $\boldsymbol{\ka} = \ka \uvec{u} = (c/\omega)\vec{k}$ est de la forme $$e^{ i \left( \vec{k} \cdot \vec{x} - \omega t \right)} = e^{ i \frac{\omega}{c}\left( \boldsymbol{\ka} \cdot \vec{x} - c t \right)} = e^{ i \frac{\omega}{c}\left( \ka \uvec{u} \cdot \vec{x} - c t \right)}.$$ Cela signifie que $\ka$ est un indice de réfraction effectif² pour l'onde plane qui se propage dans la direction $\uvec{u}$.
En général, il y a deux vitesses de propagation possibles pour chaque direction $\uvec{u}$. Cependant, pour les directions qui correspondent aux points où les deux feuillets se touchent, ces deux vitesses de propagation sont les mêmes. Ces directions, comme on le verra, sont également privilégiées au niveau de la polarisation. Étant donné leurs propriétés particulières, on leur donne le nom d'axes optiques.
En termes de type de matériau anisotrope, on constate
les faits suivants :
- Dans le cas des milieux uniaxes, le déterminant $\Delta(\boldsymbol{\ka})$ se factorise et la surface a pour équation $$(\ka^2-\eps'_1) (\eps'_1\ka_x^2+\eps'_1\ka_y^2+\eps'_3\ka_z^2 -\eps'_1\eps'_3)=0.$$ Les deux feuillets sont donc une sphère et un ellipsoïde de révolution, tangents en $\boldsymbol{\ka} = \left( 0,~0,\pm \sqrt{\eps'_1} \right)$. On a un seul axe optique, qui est l'axe des $z$.
- Dans le cas des milieux biaxes, les deux feuillets se touchent en quatre points symétriques du plan $xz$, situés sur deux droites dont les directions sont $u_y = 0$ et $$\begin{array} {ll} u_x = \pm \sqrt{ \dfrac{\eps'_3(\eps'_2-\eps'_1)}{\eps'_2(\eps'_3-\eps'_1)}}, & u_z = \pm \sqrt{ \dfrac{\eps'_1(\eps'_3-\eps'_2)}{\eps'_2(\eps'_3-\eps'_1)}}. \end{array}$$ Il y a donc deux axes optiques.
On comprend maintenant pourquoi ces deux types de milieu sont appelés respectivement « uniaxe » et « biaxe ».
² Pour cette raison, certains auteurs donnent à la surface $\Delta(\boldsymbol{\ka})=0$ le nom de « surface des indices » (à ne pas confondre avec l'ellipsoïde des indices, dont on parlera à la prochaine page).
4. Notes et références
Remarques
- On vérifie facilement que pour une onde plane, $\fvec{D}$ est perpendiculaire à $\fvec{H}$ et $\vec{k}$ et que $\fvec{H}$ est perpendiculaire à $\vec{k}$ et à $\fvec{E}$. La conséquence est que $\fvec{E}$ doit être dans le plan qui contient $\fvec{D}$ et $\vec{k}$. Puisque $\fvec{E}$ n'est pas perpendiculaire à $\vec{k}$, l'énergie se propage dans une direction qui fait un angle avec le vecteur d'onde.
- En manipulant l'équation (1), il est possible d'arriver à la relation suivante : $$\dfrac{u_x^2}{\ka^2-\eps_1}+\dfrac{u_y^2}{\ka^2-\eps_2}+\dfrac{u_z^2}{\ka^2-\eps_3}=\dfrac{1}{\ka^2}$$ connue sous le nom d'équation de Fresnel.
- Regardons ce qui se passe lorsqu'on prend une direction de propagation parallèle à un des axes principaux. Par exemple, avec $\ka_x=\ka_z=0$, le système (2) devient $$\begin{bmatrix} \eps'_1-\ka_y^2 & 0 & 0 \\ 0 & \eps'_2 & 0 \\ 0 & 0 & \eps'_3-\ka_y^2 \end{bmatrix} \begin{bmatrix} \f{E}_x \\ \f{E}_y \\ \f{E}_z \end{bmatrix} = 0.$$ La matrice des coefficients est diagonale et on a $$\begin{array} {l} \Delta(\boldsymbol{\ka}) = 0~~\Leftrightarrow~~\ka_y^2=\eps'_1~~\mathsf{ou}~~\ka_y^2=\eps'_3. \end{array}$$ Si on prend $\ka_y=\pm\sqrt{\eps'_1}$, on doit avoir $E_y=E_z=0$ et si on prend $\ka_y=\pm\sqrt{\eps'_3}$, on doit avoir $E_x=E_y=0$. Dans les directions autres qu'un axe optique, une onde plane peut se propager seulement dans des états de polarisation bien précis.
- Que se passerait-il si, dans un milieu uniaxe, on prenait $\ka_x=\ka_y=0$ ?
Nous continuerons notre étude des milieux anisotropes à la page suivante.