Calcul d'aires
Il y a un rapport étroit entre l'intégrale définie et le calcul d'aires. Les exemples présentés dans cette section nous aideront à comprendre le lien entre les deux concepts.
1 Calcul d'aire : un exemple
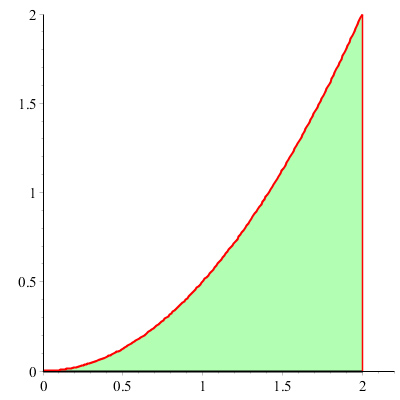
Supposons que nous voulions connaitre l'aire $A$ du triangle curviligne sur la gauche, délimité par l'axe des $x$, la droite verticale $x = 2$ et la parabole $y = \frac{x^2}{2}$. Étant donné qu'un des côtés du triangle est une courbe, nous ne connaissons pas de formule pour calculer l'aire. Cependant, nous pouvons nous inspirer de la méthode d'exhaustion et approximer ce triangle par une série de rectangles. La somme des aires des rectangles fournira une approximation de l'aire du triangle curviligne.
Nous pouvons nous organiser pour obtenir une estimation
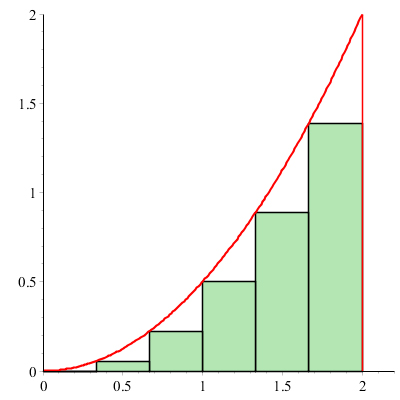
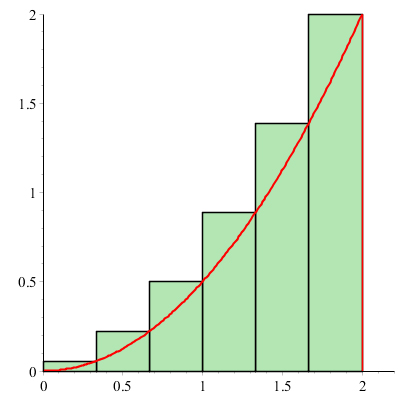
qui est soit plus petite, soit plus grande que la valeur exacte ; nous pouvons aussi améliorer la précision en augmentant le nombre de rectangles.
Cette démarche conduit à une valeur $A = 4/3$. Vous trouverez tous les détails dans le document PDF intitulé Calcul d’aire : un exemple.
2 Vidéos
Voici trois vidéos qui montrent d'autres exemples de calculs d'aires. De nouveau, poussez la touche Esc/Échap pour revenir à cette page web si vous les visionnez en plein écran.
3 Exercices
Exercice 1. Calculez les aires des triangles délimités par
a) l'axe des $x$ et les droites $y=2x$ et $x=1$;
b) l'axe des $x$ et les droites $y=-x$ et $x=1$;
c) les droites $y=2x$, $y=-x$ et $x=1$.
Exercice 2. Calculez les aires des triangles délimités par
a) l'axe des $x$ et les droites $y=x$ et $x=2$;
b) l'axe des $x$ et les droites $y=2x$ et $x=2$;
c) les droites $y=x$, $y=2x$ et $x=2$.
Exercice 3. Calculez les aires des figures délimitées par l'axe des $x$, la courbe $y=x^3$ et
a) la verticale $x=1$;
b) la verticale $x=2$;
c) les verticales $x=1$ et $x=2$.
Exercice 4. Calculez les aires des trapèzes de sommets
a) $(0, 0)$, $(0, 2)$, $(3, 4)$ et $(3, 0)$;
b) $(0, 1)$, $(0, 3)$, $(3, 5)$ et $(3, 1)$;
c) $(2, 1)$, $(2, 3)$, $(5, 5)$ et $(5, 1)$.