L'intégrale définie
Nous introduisons les sommes de Riemann et leurs limites, les intégrales définies.
1 Sommes de Riemann et intégrales
Soit $f$ une fonction définie sur l'intervalle borné $[a, b]$. Découpons cet intervalle en un nombre fini $n$ de sous-intervalles $I_i=[x_{i-1}, x_i]$. Pour la simplicité, nous les prendrons de largeur égale
$ \Delta x = \frac{b-a}{n}$ :

Dans chacun des sous-intervalles, choisissons un point arbitraire $ x_i^*$. La somme $$ \sum_{i=1}^n f(x_i^*) \Delta x $$ porte le nom de « somme de Riemann ».
Définition 1. Si, quand $n$ tend vers l'infini, les sommes de Riemann tendent vers une limite qui ne dépend pas des points $ x_i^* $ choisis, on dit que la fonction $f$ est intégrable sur l'intervalle $[a, b]$ et on écrit $$ \int_a^bf(x)~dx = \lim\limits_{n \to \infty}\sum_{i=1}^n f(x_i^*) \Delta x. $$ $ \int_a^bf(x)~dx$ s'appelle l'intégrale de $f$ sur l'intervalle $[a, b]$. On dit que la fonction $f$ est l'intégrande et que $a$ et $b$ sont les bornes (inférieure et supérieure) de l'intégrale.
Ce ne sont pas toutes les fonctions qui sont intégrables. En effet, il est facile de voir que la fonction définie par $$f(x) = \begin{cases}0 & \text{si}~x\in\mathbb{Q} \\ 1 & \text{sinon} \end{cases}$$ n'est pas intégrable, car si on choisit les $x_i^*$ rationnels, les sommes de Riemann et leur limite seront $0$, alors que si on choisit les $x_i^*$ irrationnels, les sommes de Riemann et leur limite seront $b-a$, puisque $\sum_{i=1}^n \Delta x = n \Delta x$.
Voici un théorème qui affirme l'existance de l'intégrale pour une grande classe de fonction :
Théorème 1. Si la fonction $f$ est continue par morceaux sur l'intervalle $[a, b]$, alors $ \int_a^bf(x)~dx$ existe.
Dans la suite, sauf mention explicite du contraire, on supposera que les fonctions dont on parle sont des fonctions continues par morceaux.
Remarque 1. $ \int_a^bf(x)~dx$ est un nombre bien précis qui est compètement déterminé par la fonction $f$ et les valeurs de $a$ et $b$. On dit de l'intégrale qu'il s'agit d'une intégrale définie.
Remarque 2. Le symbole $ \int$ est en fait un « s » tel qu'on l'écrivait au 17e siècle. Il rappelle que l'intégrale est une limite de sommes.
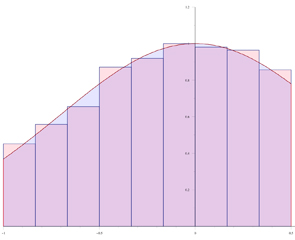
Si $f(x) \gt 0$, alors $f(x_i^*) \Delta x$ est l'aire d'un rectangle de largeur $ \Delta x$ et de hauteur $f(x_i^*)$. Si on met de tels rectangles côté à côté, on voit que la somme de leurs aires, c-à-d. la somme de Riemann $ \sum_{i=1}^n f(x_i^*) \Delta x $, approxime l'aire de la figure délimitée par l'axe des $x$, la courbe $y=f(x)$ et les droites verticales $x=a$ et $x=b$. Lorsqu'on passe à la limite, on obtient la constatation suivante :
Remarque 3. Pour une fonction $f$ positive sur l'intervalle $[a, b]$, $ \int_a^bf(x)~dx$ représente l'aire de la figure délimitée par l'axe des $x$, le graphe de la fonction $f$ et les droites verticales $x=a$ et $x=b$.
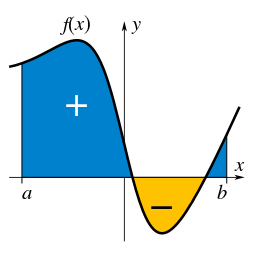
Si la fonction n'est pas positive, alors l'intégrale représente une aire algébrique : il faut compter les aires au dessus de l'axe des $x$ positivement et les aires sous l'axe des $x$ négativement, comme dans la figure à droite.
2 Vidéos
3 Exercices
Exercice 1. Soit $f$ une fonction dont les valeurs sont données dans le tableau suivant :
| $x$ | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1 |
|---|---|---|---|---|---|---|
| $f(x)$ | 1 | 3 | 2 | 4 | 3 | 5 |
Calculez une valeur approximative de $\int_{0}^{1} f(x)~dx$.
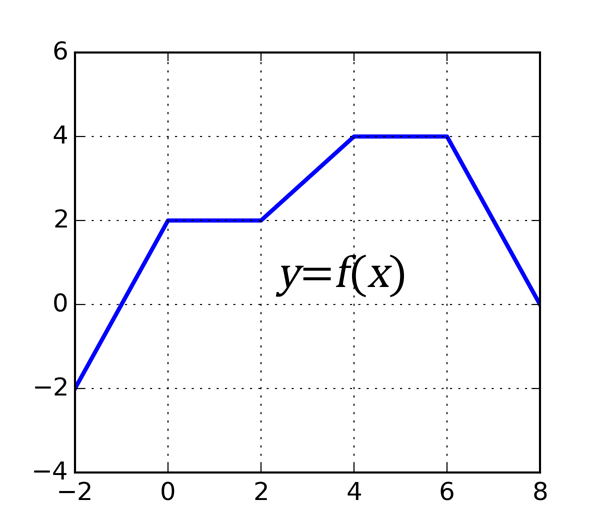
Exercice 2. Soit $f$ la fonction dont le graphe, représenté à gauche, est formé de segments de droites. Calculez
a) $\int_{2}^{6} f(x)~dx$;
b) $\int_{-2}^{8} f(x)~dx$.
Exercice 3. Calculez des bornes supérieure et inférieure pour $\int_{0}^{3} g(x)~dx$ si $g$ une fonction croissante dont les valeurs sont données dans le tableau
| $x$ | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 |
|---|---|---|---|---|---|---|---|
| $g(x)$ | 1.2 | 2 | 2.4 | 3 | 3.6 | 4 | 4.8 |
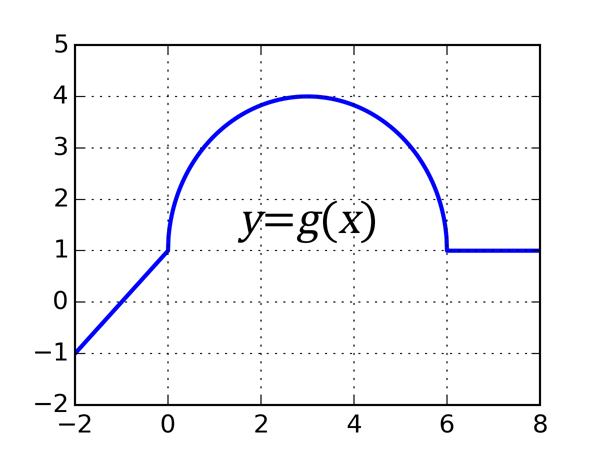
Exercice 4. Soit $g$ la fonction dont le graphe, représenté à gauche, est formé de deux segments de droites et d'un demi-cercle. Calculez
a) $\int_{1}^{3} g(x)~dx$;
b) $\int_{-2}^{8} g(x)~dx$.