Calcul de l'aire entre deux courbes
On a vu que, pour une fonction positive, l'intégrale représentait l'aire entre le graphe de la fonction et l'axe des $x$. L'intégrale peut aussi être utilisée pour calculer l'aire d'une région située entre les graphes de deux fonctions.
1 Aire entre des courbes y = f(x) et y = g(x)
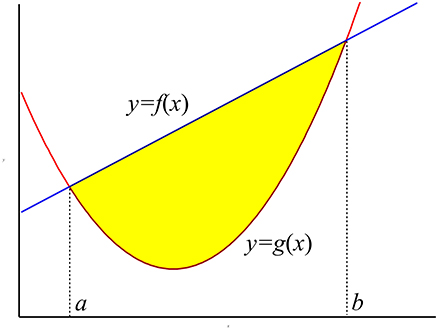
Supposons qu'on veuille calculer l'aire de la région située entre deux courbes $y=f(x)$ et $y=g(x)$. Une situation courante est le cas où les deux courbes se coupent deux fois : il est alors sous- entendu que l'aire qu'on cherche est celle qui est située entre les points d'intersection, comme l'aire en jaune dans la figure du haut à gauche. La première tâche est alors de trouver les abscisses $a$ et $b$ des points d'intersection.
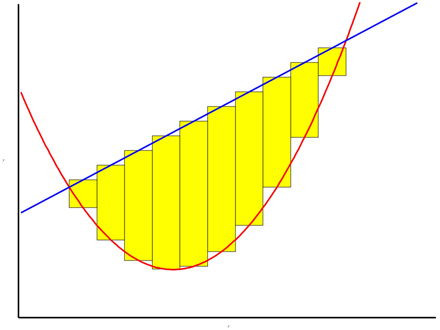
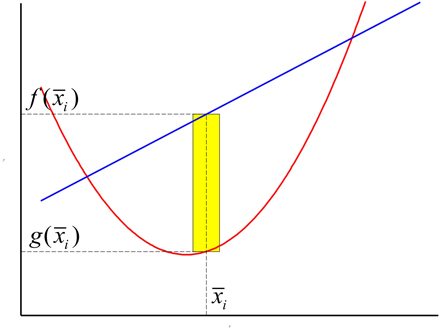
La tâche suivante consiste à découper l'intervalle $[a, b]$ en $n$ sous-intervalles de largeur égale $\Delta x$ et à approximer l'aire avec des rectangles, tout comme on l'a fait pour les calculs d'aire au début du cours. Ces rectangles auront tous une largeur $\Delta x$ et leur hauteur sera déterminée en choisissant dans chaque sous- intervalle un point $x_i^*$ et en mesurant la distance verticale $f(x_i^*) - g(x_i^*)$ entre les deux courbes pour cette valeur de $x$. Un de ces rectangles est représenté dans la figure du bas (on a choisi $x_i^* = \overline{x}_i$, point milieu de l'intervalle, mais d'autres choix sont bien entendu possibles).
L'aire entre les courbes sera donc approximée par la somme des aires des
rectangles :
$A_n = \sum_{i=1}^n \left[ f(x_i^*) - g(x_i^*) \right] \Delta x$.
On reconnait là une somme de Riemann. En faisant tendre $n$ vers l'infini, on obtiendra l'aire exacte :
$A = \int_a^b \left[ f(x) - g(x) \right] ~dx$.
Exemple 1. On veut calculer l'aire de la région située entre la parabole $y = x^2-4x+5$ et la droite $y = x+1$. Tout d'abord, cherchons les points d'intersection des deux courbes : on a
$~~~~~~x^2-4x+5 = x+1 \iff \\x^2-5x+4 = 0 \iff x=1,~4.$
On constate qu'entre $x=1$ et $x=4$, la droite est située au-dessus de la parabole. La réponse sera donc fournie par l'intégrale
$\int_1^4 \left[ (x+1)-(x^2-4x+5) \right]~dx \\ ~~~~~~~~~ =\int_1^4 (-x^2+5x-4)~dx \\ ~~~~~~~~~ =\left[ - \dfrac {x^3} {3} +5 \dfrac {x^2} {2}-4x \right]_1^4 \\ ~~~~~~~~~ = \dfrac {8} {3} + \dfrac {11} {6} =\dfrac {9} {2}.$
2 Aire entre des courbes x = h(y) et x = k(y)
Dans certains cas, les courbes auront plutôt pour équations $x=h(y)$ et $x=k(y)$. La situation sera sensiblement la même que plus haut, sauf qu'on utilisera $y$ comme variable : si les courbes se croisent en $y=c$ et $y=d$, on découpera l'intervalle $[c, d]$ en $n$ sous-intervalles et l'aire entre les courbes sera approximée en utilisant des rectangles de hauteur $\Delta y$ et de largeur égale à la distance horizontale $\left| h(y_i^*) - k(y_i^*) \right|$ entre les deux courbes, $y_i^*$ étant une valeur choisie dans le $i$ème sous- intervalle. On obtiendra ainsi l'approximation
$A_n = \sum_{i=1}^n \left| h(y_i^*) - k(y_i^*) \right| \Delta y$
qui, en passant à la limite $n \to \infty$, conduira à la valeur exacte
$A = \int_c^d \left| h(y) - k(y) \right| ~dy$.
Il peut arriver que le calcul puisse se faire des deux manières, comme dans l'exemple suivant.
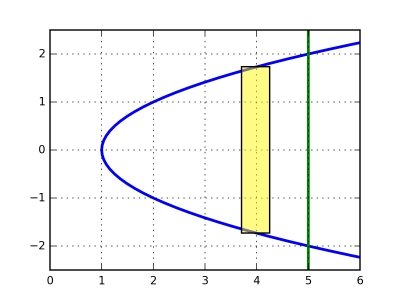
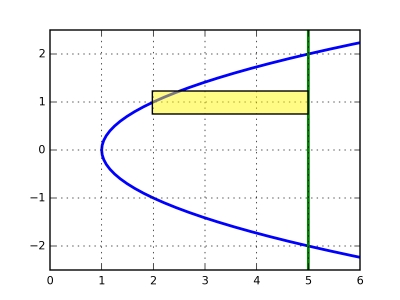
Exemple 2. On veut calculer l'aire de la région située entre la parabole $x = y^2 + 1$ et la droite $x = 5$. On peut considérer qu'il s'agit de l'aire entre les courbes $y = -\sqrt{x-1}$ et $y = \sqrt{x-1}$ pour $x$ entre $1$ et $5$.
Donc, la réponse sera
$\int_1^5 2\sqrt{x-1}~dx = 2\int_0^4 \sqrt{u}~du = 2\left[ \dfrac {2} {3} u^{3/2} \right]_0^4 = \dfrac {32} {3}$.
On peut aussi considérer qu'il s'agit de la région entre les courbes $x = y^2+1$ et $x = 5$ qui se croisent en $y = \pm 2$. La réponse doit donc être aussi fournie par l'intégrale
$\int_{-2}^2 \left[ 5-\left( y^2+1 \right) \right]~dy = \int_{-2}^2 (4-y^2)~dy \\ ~~~~~~~~~~ = \left[ 4y- \dfrac {y^3} {3} \right]_{-2}^2 = \dfrac {16} {3} + \dfrac {16} {3} = \dfrac {32} {3}.$
On obtient bien sûr le même résultat !
3 Vidéos
4 Exercices
Exercice 1. Calculez l’aire de la région $R$ délimitée par la parabole $y=x^2-2x+1$ et la droite $y=2x-2$.
Exercice 2. Calculez l’aire de la région $R$ délimitée par la parabole $y=x^2-3x$ et la droite $y=3x-5$.
Exercice 3. Calculez l’aire de la région $R$ située entre la demi-parabole $y=\sqrt{x}$ et la droite $y=\dfrac{x+2}{3}$.
Exercice 4. Calculez l’aire de la région $R$ délimitée par les droites $y=x$, $y=1$ et $y=2x$.
Exercice 5. Calculez l’aire de la partie du plan $P$ située entre la courbe $y=\sqrt[3]{x}$ et la droite $y=x/4$ (attention : $P$ est composée de deux régions distinctes).
Exercice 6. Calculez l’aire de la région $R$ située entre les paraboles $x=2y^2-2$ et $x=y^2+y$.