Calcul de volumes par les tranches
Voici une méthode assez générale pour calculer le volume de certains solides, qui consiste à les découper en tranches ou rondelles.
1 Calcul de volumes par les tranches

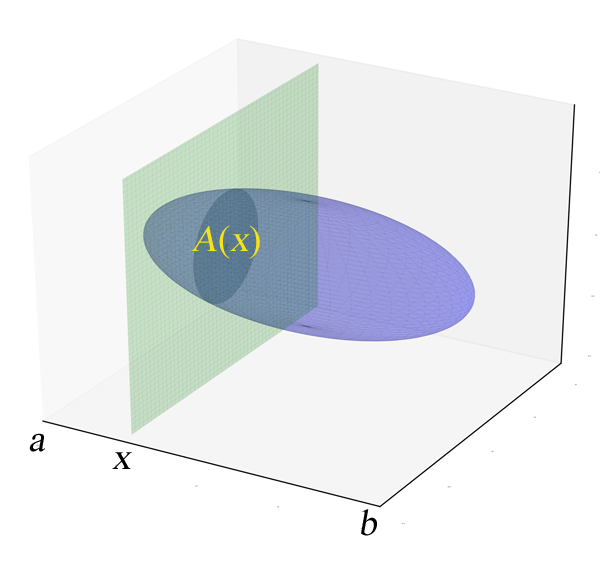
Supposons qu'on veuille calculer le volume d'un solide, comme par exemple l'ellipsoïde dans la figure 1 à gauche. Une manière de faire consiste à imaginer un axe des $x$ situé le long du solide et à balayer le solide avec un plan qui se déplace perpendiculairement à l'axe. La situation est illustrée dans la figure 2 : on voit que la valeur $x$ où le plan coupe l'axe varie entre deux valeurs extrêmes $a$ et $b$; on désignera par $A(x)$ l'aire de la section du solide par le plan.
Imaginons maintenant que nous découpions l'intervalle $[a, b]$ en $n$ sous-intervalles $[x_{i-1}, x_i]$ de largeur constante
$\Delta x = x_i-x_{i-1} \\ ~~~~~= \dfrac {b-a} {n}.$
Les plans qui croisent l'axe aux valeurs $ x_i$ découpent le solide en un nombre $n$ de tranches ou rondelles qui ont des faces parallèles et une épaisseur $\Delta x$. Si on désigne le volume de chacune de ces rondelles par $V_i$, le volume du solide sera
$$V = \sum_{i=1}^n V_i.$$
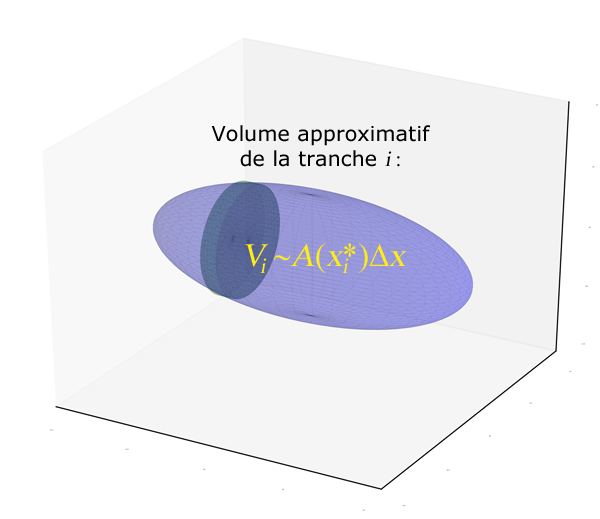
Si, dans chacun des sous-intervalles, on choisit un point arbitraire $x_i^*$, le volume de la ième rondelle
sera approximativement $$V_i \approx A(x_i^*) \Delta x$$ (voir figure 3). On aura donc
$$V \approx \sum_{i=1}^n A(x_i^*) \Delta x.$$
On reconnait là une somme de Riemann. Cela veut dire que si $A(x)$ est une fonction continue de $x$, en prenant la limite $n \to \infty$, on aura
$$V = \int_a^b A(x) ~dx.$$
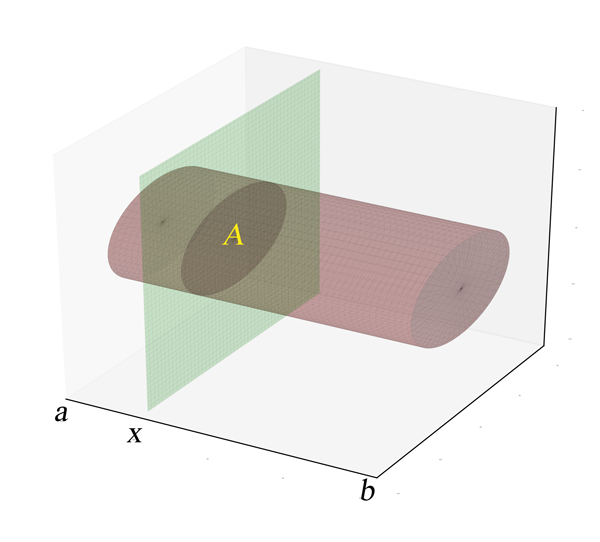
Exemple 1. Un cas particulier courant est celui des cylindres et des prismes. Si on prend l'axe perpendiculaire aux bases, l'aire des sections est une constante $A$ et on a
$V = \int_a^b A~dx=(b-a)A$
c.-à-d., en posant $h=b-a$,
$$V = Ah.$$
Donc, pour un prisme ou un cylindre, volume = aire de la base × hauteur.
2 Pyramides et cônes
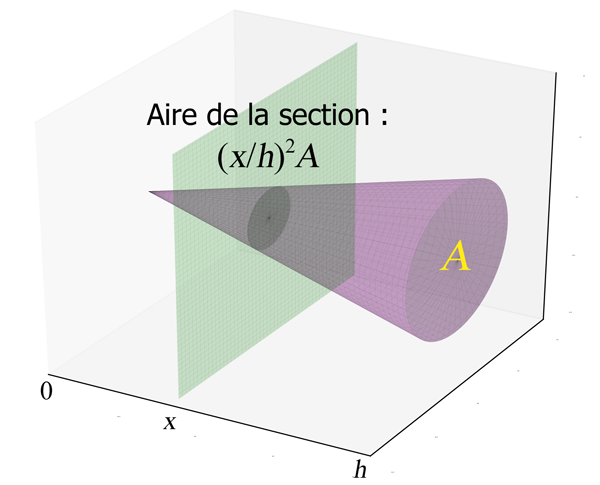
Exemple 2. Un autre exemple courant est fourni par les pyramides et les cônes. Si on prend l'axe perpendiculaire à la base, il est clair que les sections seront semblables à la base. En mettant le sommet à $x=0$ et la base à $x=h$, comme dans la figure 5 à gauche, le facteur de proportionnalité pour les longueurs sera
$x/h$. Il s'ensuit que si l'aire de la base est $A$, l'aire des sections sera $(x/h)^2A$. On aura donc
$V = \int_0^h (x/h)^2A~dx \\ ~~~= \dfrac {A}{h^2}\int_0^h x^2~dx \\ ~~~= \dfrac {A}{h^2}\dfrac {h^3}{3} = \dfrac {1}{3}Ah$
La règle est donc que le volume d'un cône ou d'une pyramide est égal au tiers de l'aire de la base fois la hauteur.
3 Solides de révolution
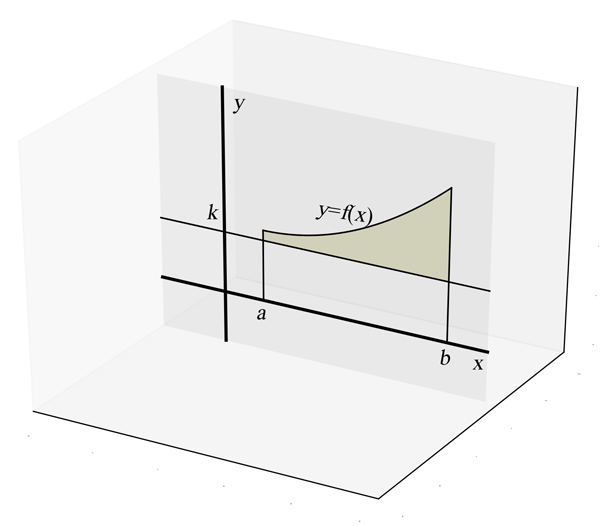
la région de la fig. 6 autour de la droite $y=k$.
Définition 1. Un solide de révolution est un solide engendré en faisant tourner une région d'un plan autour d'une droite du même plan.
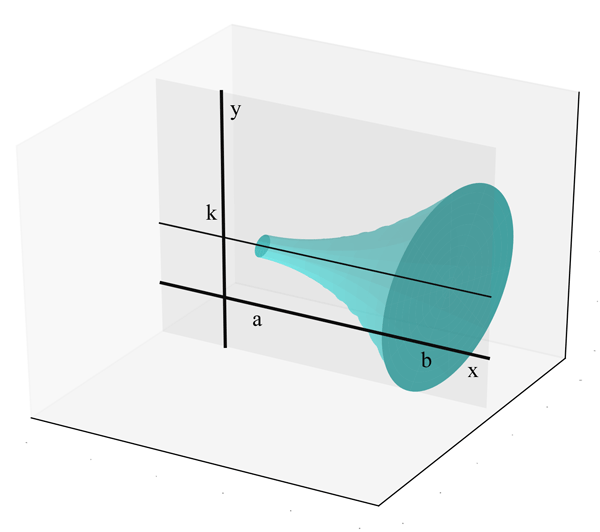
Exemple 3. Dans la figure 6, on a en beige une région du plan $xy$ délimitée par la courbe $y=f(x)$ et les droites $x=a$, $x=b$ et $y=k$. Si on fait tourner cette région autour de la droite $y=k$, on obtient le solide de révolution représenté à la figure 7. Dans ce cas les sections seront des disques de rayon $r = |f(x)-k|$ et donc d'aire $A(x) = \pi r^2 = \pi [f(x)-k]^2$. On aura donc
$V = \int_a^b A(x)~dx = \pi \int_a^b [f(x)-k]^2~dx.$
Si, par exemple, on faisait tourner la même région autour de l'axe des $x$, le solide engendré aurait un « trou » et les sections seraient maintenant des anneaux de rayon intérieur $r_i = k$ et de rayon extérieur $r_e = f(x)$. On aurait donc $A(x) = \pi (r_e^2-r_i^2) = \pi [f^2(x)-k^2]$, d`où
$V = \int_a^b A(x)~dx = \pi \int_a^b [f^2(x)-k^2]~dx.$
Remarque 1. On peut tenir le même type de raisonnement lorsqu'on fait tourner une région du plan autour d'une droite verticale. Dans ce cas, on prendra $y$ comme variable d'intégration et on aura comme formule pour le volume
$V = \int_c^d A(y)~dy.$
4 Vidéos
Vous trouverez deux pages plus loin des vidéos sur le calcul de volumes.
5 Exercices
À venir.