Solides de révolution : calcul du volume par les tubes
Voici une autre méthode de calcul de volumes qui peut être utilisée avec les solides de révolution. Elle consiste à découper ces solides en tubes.
1 Décomposition d'un solide de révolution en tubes
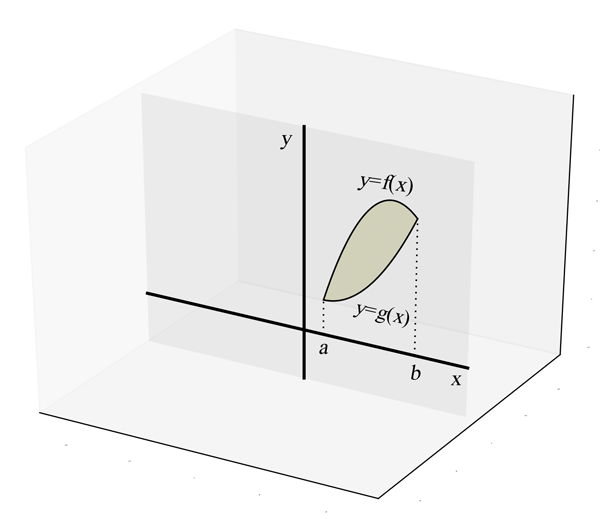

de la fig. 1 par des rectangles.

la région de la fig. 1 autour de l'axe des $y$.
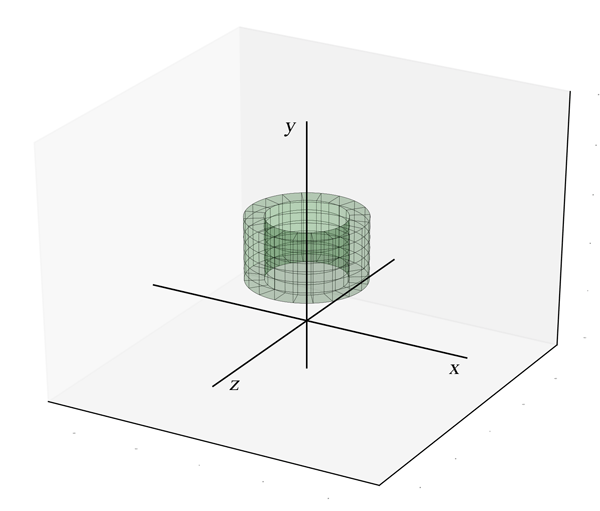
rectangles de la fig. 3 autour de l'axe des $y$.
Pour calculer le volume du solide de la figure 2 à gauche, engendré par la révolution de la région de la figure 1 autour de l'axe des $y$, la méthode des tranches pourrait s'avérer compliquée. Il faudrait utiliser des tranches horizontales annulaires et le calcul des rayons de ces anneaux pourrait être d'autant plus difficile que la fonction $f$ n'est pas inversible.
Heureusement, une autre avenue s'ouvre à nous. On a vu comment, pour calculer l'aire de la région en question, on peut utiliser une approximation avec des rectangles de même largeur comme dans la figure 3. Le solide de révolution engendré par la rotation d'un de ces rectangles est représenté à la figure 4 : il s'agit d'un tube. Si on ajoute les volumes de tous ces tubes, on obtiendra approximativement le volume du solide de la figure 2.
2 Calcul de volumes par les tubes
Chacun de ces tubes est un cylindre circulaire avec au centre un vide, lui aussi cylindrique. La base est donc un anneau. Si on désigne par $r_{ext}$ et $r_{int}$ les rayons extérieur et intérieur d'un tube et par $h$ sa hauteur, son volume sera donné par la formule
$V_{tube} = \pi \left(r_{ext}^2-r_{int}^2 \right) h$.
En utilisant l'identité $r_{ext}^2-r_{int}^2$ $=$ $(r_{ext}-r_{int})$ $\times$ $(r_{ext}+r_{int})$ et en définissant $\Delta r = r_{ext}-r_{int}$ et $\bar{r}= (r_{ext}+r_{int})/2$, la formule devient
$V_{tube} = 2\pi \bar{r} \Delta r h$.
Si nous avons découpé l'intervalle $[a, b]$ en $n$ sous-intervalles $[x_{i-1}, x_i]$ de largeur constante
$\Delta x = x_i-x_{i-1} = \dfrac {b-a} {n}$,
on aura pour le ième tube $r_{int}=x_{i-1}$, $r_{ext}=x_i$ et donc $\Delta r = \Delta x$ et $\bar{r}=\bar{x}_i$, milieu du ième sous-intervalle. En choisissant $h = f(\bar{x}_i)-g(\bar{x}_i)$, on obtient pour le ième tube le volume
$V_i = 2\pi \bar{x}_i \left( f(\bar{x}_i)-g(\bar{x}_i) \right) \Delta x$.
et le volume du solide de révolution sera approximativement
$V = \sum_{i=1}^n V_i.$
c.-à-d.
$V = \sum_{i=1}^n 2\pi \bar{x}_i \left( f(\bar{x}_i)-g(\bar{x}_i) \right) \Delta x$.
Si maintenant on fait tendre $n$ vers l'infini et si les fonctions $f$ et $g$ sont continues, on aura à la limite
$V = 2\pi \int_a^b x \left( f(x)-g(x) \right)~dx$.
Cette formule a en fait la forme
$V = 2\pi \int_a^b r(x) h(x)~dx$
où $r(x)$ est la distance entre $x$ et l'axe de rotation et $h(x)$ est la hauteur de la région qu'on fait tourner pour la valeur $x$.
Problème 1. Calculer le volume du solide de
révolution obtenu en faisant tourner autour de l'axe $y$ la région délimitée par la parabole $y=$ $-4x^2$ $+24x$ $-32$ et l'axe des $x$.
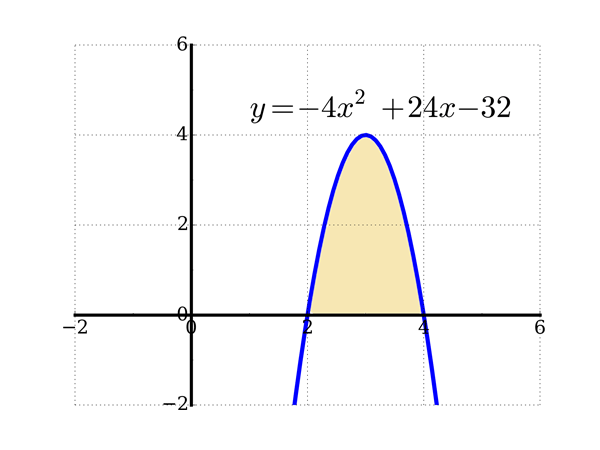
Solution : Dans ce cas-ci, on a $f(x)$ $=$ $-4x^2$ $+$ $24x-32$ et $g(x)=0$. On constate dans la figure à droite que la parabole intersecte l'axe des $x$ en $x=2$ et $x=4$ La formule donne donc
$V = 2\pi \int_2^4 x \left(-4x^2+24x-32 \right)dx \\ ~~~= -8\pi \int_2^4 \left(x^3-6x^2+8x \right)dx = 32 \pi$.
Problème 2. Calculer le volume du solide de révolution obtenu en faisant tourner le trapèze de sommets $(2, 1)$, $(4, 1)$, $(4, 3)$ et $(2, 2)$ autour de la droite $x = 1$.
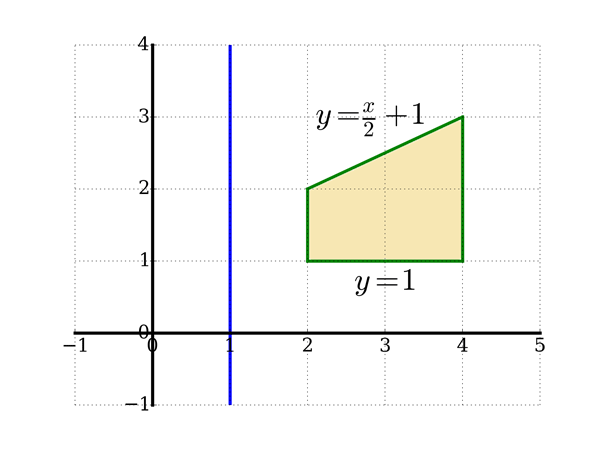
Solution : Ici, on a $a=2$, $b=4$, $f(x)$ $=$ $\dfrac {x}{2}+1$ et $g(x)=1$, ce qui donne $h(x) = x/2$. Puisqu'on fait tourner le trapèze autour de la droite $x=1$, on a $r(x)=x-1$. Donc,
$V = 2\pi \int_2^4 (x-1)\dfrac{x}{2}~dx = \dfrac{38 \pi}{3}$.
Remarque 1. On peut aussi utiliser cette technique pour calculer le volume d'un solide de révolution avec un axe horizontal. Dans ce cas, il faut utiliser $y$ comme variable d'intégration et la formule devient
$V = 2\pi \int_c^d r(y) h(y)~dy$
3 Vidéos
Vous trouverez à la page suivante des vidéos sur le calcul de volumes.
4 Exercices
À venir.