Le théorème fondamental
Le théorème fondamental fait le lien entre le calcul différentiel et le calcul intégral.
1 Le théorème fondamental
Soit $f$ une fonction continue sur un intervalle $[a, b]$. On peut utliser l'intégration pour lui associer une fonction $F$ définie sur le même intervalle par la formule
$F(x) = \int_a^x f(t)~dt$.
Cette fonction $F$ est très particulière : on peut montrer
qu'elle est dérivable sur l'intervalle $]a, b[$ et que sa dérivée n'est autre que $f$ : c'est le théorème fondamental du calcul différentiel et intégral.
Théorème 1. Soit $f$ une fonction continue sur l'intervalle $[a, b]$. La fonction
$F(x) = \int_a^x f(t)~dt~(a \le x \le b)$
est continue sur $[a, b]$, dérivable sur $]a, b[$ et
$F'(x) = f(x)~(a \lt x \lt b)$.
Remarque 1. Le résultat du théorème 1 peut s'écrire
$\dfrac{d}{dx} \left [\int_a^x f(t)~dt \right ] = f(x)$
Il exprime que, d'une certaine manière, intégration et dérivation sont deux opérations inverses l'une de l'autre.
Remarque 2. Si la fonction $f$ était seulement continue par morceaux sur l'intervalle $[a, b]$, le graphe de la fonction $F$ aurait alors des points anguleux aux valeurs de $x$ où $f$ fait des sauts.
Il résulte du théorème 1 que si $f$ est une fonction continue sur un intervalle ouvert $I$ qui contient le point $a$,
alors la fonction $F$ définie par
$F(x) = \int_a^x f(t)~dt$
est une primitive de $f$ sur $I$. Ceci, joint aux résultats de la section précédente, entraîne la formule de Newton-Leibniz :
Théorème 2. Soit $f$ une fonction continue sur l'intervalle ouvert $I$ et soit $F$ une primitive quelconque de $f$ sur $I$. Pour $a$ et $b$ dans $I$, on a
$\int_a^b f(x)~dx = F(b)-F(a)$.
Preuve : Posons $G(x) = \int_a^x f(t)~dt$. On a $G(a) = 0$, et donc
$\int_a^b f(t)~dt = G(b) = G(b)-G(a)$.
Si $F$ est une autre primitive de $f$ sur $I$, on doit avoir $G(x) = F(x)+C$ pour une certaine constante $C$, d'où
$\begin{align} G(b)-G(a) & = F(b)+C-[F(a)+C] \\ & = F(b)-F(a). \\ \end{align}$
On a donc
$\int_a^b f(x)~dx = \int_a^b f(t)~dt = F(b)-F(a)$.
Définition 1. On définit la variation de $F$ entre $a$ et $b$ par
$F(x) \big|_a^b = F(b)-F(a)$.
On utilise aussi la notation $ \big[F(x)\big]_a^b $.
Avec ces notations, la formule de Newton-Leibniz s'écrit
$\int_a^b f(x)~dx = F(x)\big|_a^b$
ou encore
$\int_a^b f(x)~dx = \big[F(x)\big]_a^b$.
Exemple 1. $\frac {1} {4} x^4$ est une primitive de $x^3$ sur $\mathbb{R}$, donc
$\int_1^2 x^3~dx = \big[\frac {1} {4} x^4\big]_1^2 = \frac {15} {4}$.
2 Vidéos
3 Exercices
Exercice 1. Déterminez laquelle des fonctions suivantes pourrait être égale à $\int_0^x 3t^5~dt$
| a) $15x^4$; | b) $x^6/2$; | c) $3x^5/5$; |
| d) Aucune de ces réponses. | ||
Exercice 2. Calculez $f'(x)$ et $f"(x)$ si
| a) $f(x)= \int_0^x e^{2t}~dt$; | b) $f(x)= \int_x^0 e^{2t}~dt$; |
| c) $f(x)= \int_0^{x^2} e^{2t}~dt$; | d) $f(x)= \int_{3x}^{x^2} e^{2t}~dt$. |
Exercice 3. Soit $f$ une fonction continue et soit $g(x)=\int_{0}^{x} f(t)~dt$. Que peut on dire de $f$ sur un intervalle $I$ où $g$ est a) croissante; b) décroissante ?
Exercice 4. Soit $g(x)=\int_{0}^{x} f(t)~dt$ où $f$ est la
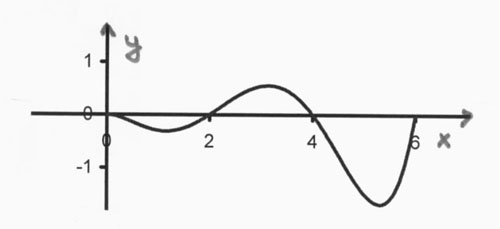
a) Déterminez pour quelle(s) valeur(s) de $x$ la fonction $g$ a un maximum local;
b) Déterminez pour quelle(s) valeur(s) de $x$ la fonction $g$ a un minimum local;
c) Où $g$ atteint-elle son maximum absolu ?
d) Où $g$ atteint-elle son minimum absolu ?