Longueur d'un arc de courbe
1èrepartie : graphes de fonctions
Nous allons tout d'abord calculer la longueur pour des arcs de courbes qui sont de la forme $y=f(x)$ ou $x=g(y)$.
1 Courbes de la forme y = f(x) ou x = g(y)
Considérons dans le plan une courbe qui est le graphe d'une fonction $f$ définie sur l'intervalle $[a, b]$. On voudrait calculer la longueur de cette courbe. Pour ce faire, nous allons approximer la courbe par une ligne brisée formée de $n$ segments et calculer la longueur de cette ligne brisée. Nous obtiendrons ensuite la longueur exacte de la courbe par un processus de limite.
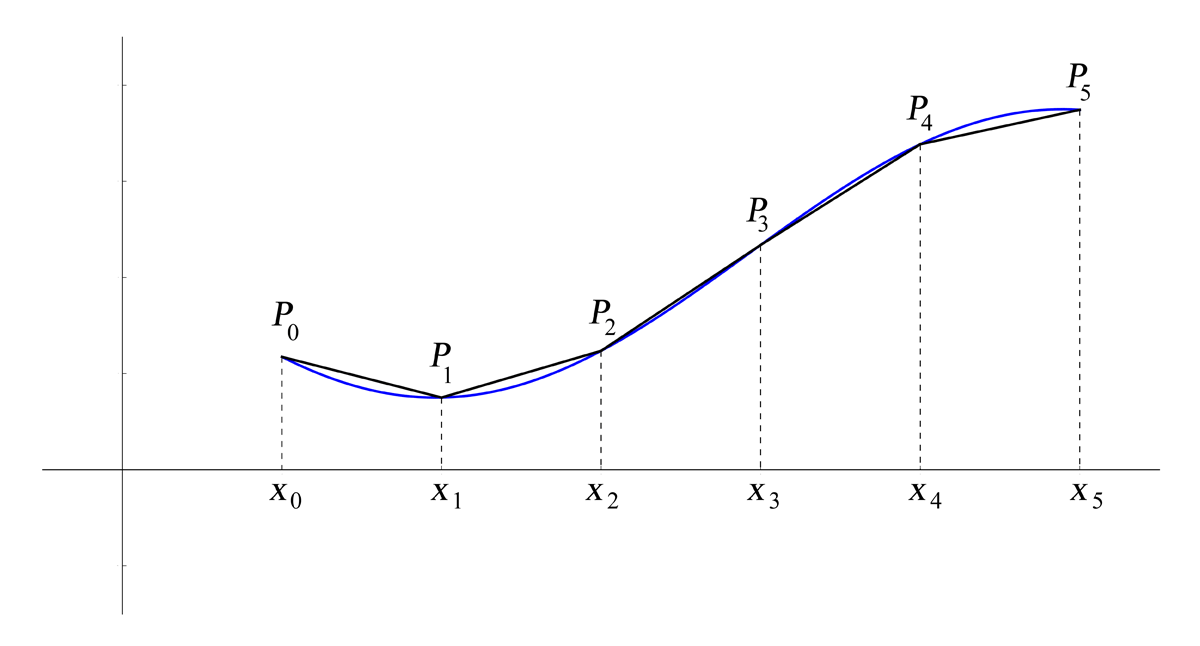
Pour réaliser notre programme, commençons selon notre habitude par diviser l'intervalle $[a, b]$ en $n$ sous-intervalles $[x_{i-1}, x_i]$ de largeur égale $\Delta x = (b-a)/n$, avec $x_0 = a$ et $x_n = b$. Pour chaque valeur de $i$ entre $0$ et $n$, nous allons considérer sur le graphe le point $P_i = (x_i, f(x_i))$. La ligne brisée que nous utiliserons sera celle formée des $n$ segments $P_{i-i}P_i$.

La situation est illustrée dans les figures 1 et 2 : on y voit le graphe de la fonction en bleu et la ligne brisée en noir.
Désignons par $\Delta s_i$ la longueur de la portion du graphe située au-dessus du ième sous-intervalle et par $L$ la longueur totale du
graphe : on aura
$L = \sum_{i=1}^n \Delta s_i$.
Si le segment $P_{i-i}P_i$ est une bonne approximation du graphe pour $x$ entre $x_{i-i}$ et $x_i$ (et l'approximation sera d'autant meilleure que $n$ sera grand), on aura $\Delta s_i \approx d(P_{i-i}, P_i)$ (voir figure 2). Sachant que $x_i-x_{i-i}= \Delta x$, en posant $y_i-y_{i-i}= \Delta y_i$ on aura
$d(P_{i-i}, P_i) = \sqrt{(\Delta x)^2+(\Delta y_i)^2} = \sqrt{1+\left(\dfrac{\Delta y_i}{\Delta x} \right)^2}~\Delta x$
et donc
$L \approx \sum_{i=1}^n d(P_{i-i}, P_i) = \sum_{i=1}^n \sqrt{1+\left(\dfrac{\Delta y_i}{\Delta x} \right)^2}~\Delta x$.
Si $f$ est dérivable, d'après le théorème des accroissements finis, il y aura dans chacun des sous-intervalles i un point $x_i^*$ tel que $\Delta y_i = f'(x_i^*) \Delta x$, d'où
$L \approx \sum_{i=1}^n d(P_{i-i}, P_i) = \sum_{i=1}^n \sqrt{1+\left(f'(x_i^*) \right)^2}~\Delta x$,
expression dans laquelle on reconnait une somme de Riemann.
Si maintenant $f'$ est continue, cette somme convergera vers une intégrale quand $n$ tend vers l'infini :
$L = \int_a^b \sqrt{1+\left(f'(x) \right)^2}~dx = \int_a^b \sqrt{1+\left(\dfrac{dy}{dx} \right)^2} ~dx$.
Remarque 1. Pour une courbe de la forme $x=g(y)$ $(c \le y \le d)$ où $g$ est continûment dérivable, la longueur est obtenue en utilisant la formule
$L = \int_c^d \sqrt{1+\left(g'(y) \right)^2}~dy = \int_c^d \sqrt{1+\left(\dfrac{dx}{dy} \right)^2} ~dy$.
2 Applications
Problème 1. Calculez la longueur de la courbe $y=3x^{2/3}-10$ entre les points $(8, 2)$ et $(27, 17)$.
Solution : Ici on a $f(x)=3x^{2/3}-10$ avec $a = 8$ et $b = 27$. Puisque $f'(x) = 2x^{-1/3}$, on a
$L = \int_8^{27} \sqrt{1+4x^{-2/3}}~dx = \int_8^{27} x^{-1/3} \sqrt{x^{2/3}+4}~dx$.
En faisant le changement de variable $u = x^{2/3}+4$ $\implies$ $du = \dfrac{2}{3} x^{-1/3} dx$ et en notant que $u$ varie de $8$ à $11$ quand $x$ varie de $8$ à $27$, on obtient
$L = \dfrac{3}{2} \int_8^{11} \sqrt{u}~du = u^{3/2} \big|_8^{11} = 11\sqrt{11} - 8\sqrt{8}$.
Problème 2. Montrez la longueur du cercle trigonométrique $x^2+y^2=1$ est bien $2 \pi$.
Solution : Le cercle trigonométrique n'est pas le graphe d'une fonction (il ne passe pas le « test de la verticale »). Il faut donc le décomposer en deux courbes qui sont des graphes de fonctions, soit la moitié supérieure $y = \sqrt{1-x^2}$ et la moitié inférieure $y = -\sqrt{1-x^2}$, avec $-1 \le x \le 1$ dans les deux cas. Pour la moitié supérieure, on a $f(x) = \sqrt{1-x^2}$, donc $f'(x) = \dfrac{-x}{\sqrt{1-x^2}}$. Cela donne
$L = \int_{-1}^{1} \sqrt{1+\left(f'(x) \right)^2}~dx = \int_{-1}^{1} \dfrac{1}{\sqrt{1-x^2}}~dx \\ ~~~~= \text{arcsin}~x~ \big|_{-1}^1 = \pi.$
Le calcul pour la moitié inférieure est similaire et donne une réponse identique. La longueur du cercle trigonométrique est donc, sans surprise, $\pi+\pi=2\pi$.
3 Vidéo
4 Exercices
Exercice 4. Montrez que si on calcule la longueur d'un segment de droite, on obtient la distance entre ses extrémités.