Variables aléatoires continues
Un des grand domaines d'application du calcul intégral est la théorie des probabilités. Nous allons voir quelques notions relatives aux variables aléatoires continues.
1 Mise en contexte

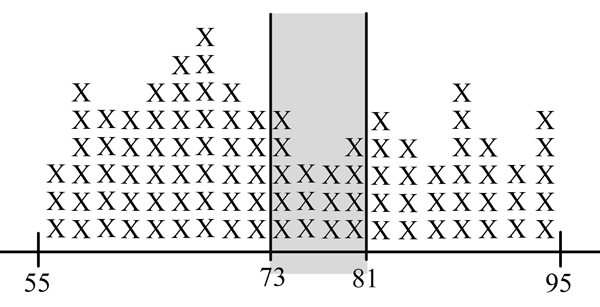
Un professeur vient de terminer la correction d'examens de calcul intégral. Les notes varient de 55.1 à 94.7. Pour avoir une idée plus précise de leur répartition, le professeur trace un graphique où des notes sont représentées par des X disposés en colonnes. Dans la colonne de gauche figurent les notes entre 55 et 57, dans la suivante les notes de 57 à 59, etc. Le graphique est reproduit à la figure 1. On y constate qu'il y a 96 copies.
une courbe. L'aire de la surface sous la courbe vaut 1.
probabilité d'avoir une note entre 73 et 81.
Intéressons-nous maintenant aux notes entre 73 et 81. Elles correspondent à la zone en gris dans la figure 2. Si on choisit une copie au hazard, quelle est la probabilité que sa note soit dans cette plage ? La réponse est simple : il y a 15 X dans la zone en gris alors qu'il y en a 96 au total. La probabilité est donc 15/96 ≈ 15.6%.
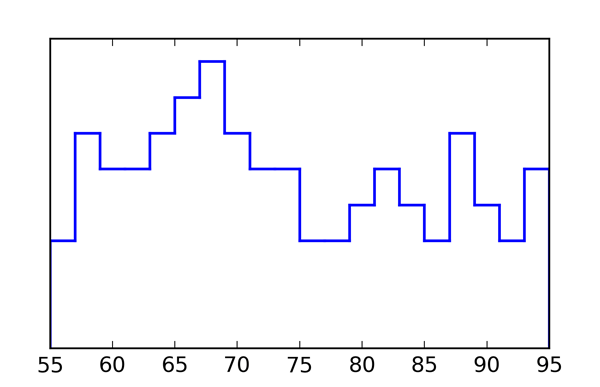
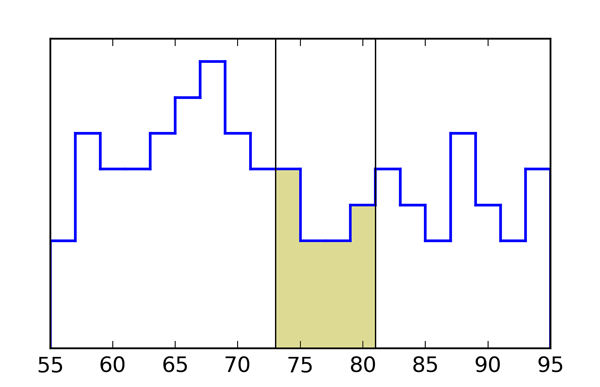
La même information peut être donnée par une courbe : traçons la ligne brisée qui enveloppe les colonnes de X, en adoptant une échelle verticale telle que chaque X couvre une surface d'aire 1/96 (figure 3) : l'aire de la surface totale sous la courbe sera alors exactement 1. Si maintenant on trace deux droites verticales en $x=73$ et $x = 81$ (figure 4), l'aire sous la courbe entre ces deux verticales sera celle qui correspond aux 15 X de la zone en gris dans la figure 2, soit de nouveau 15/96 ≈ 15.6%.
On est donc amené, en traçant une courbe à une échelle appropriée, à représenter des probabilités par des aires de surfaces sous une courbe. Puisque ces aires peuvent être obtenues par le calcul intégral, on est donc amené à associer probabilités et intégrales.
2 Variables aléatoires continues
Intuitivement, on peut voir une variable aléatoire comme un nombre qui dépend du hazard. Dans certains cas, les valeurs que peut prendre ce nombre sont des valeurs bien précises. On dit alors qu'on a une variable aléatoire discrète. Dans d'autres cas, au contraire, ces valeurs peuvent varier de manière continue, au point où la probabilité d'avoir une valeur précise déterminée à l'avance est nulle. On parle alors de variable aléatoire continue.
Exemple 1. L'exemple type d'une variable aléatoire discrète est fourni par le lancer d'un dé : les résultats possibles sont les entiers de 1 à 6, chacun avec une probabilité d'un sixième.
Exemple 2. Voici des exemples de variables aléatoires continues :
- La taille exacte d'une personne adulte choisie au hazard au Nouveau-Brunswick;
- Le poids exact d'un québecois ou d'une québecoise pris(e) au hazard;
- La durée de vie d'une lampe de 100W fabriquée dans une certaine usine.
Remarque 2. Il est habituel d'arrondir la taille d'un individu au cm près, mais quand on parle de la taille exacte, il s'agit vraiment d'une quantité qui varie continûment. Une remarque similaire s'applique au poids.
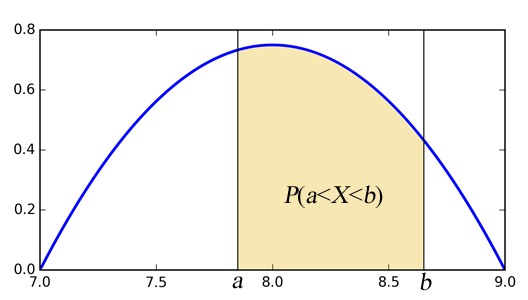
La densité de probabilité d'une variable aléatoire continue permet de calculer la probabilité que sa valeur soit dans un intervale $]a, b[$ donné :
Définition 1. On dit que la fonction $f$ est la densité de probabilité de la variable aléatoire continue $X$ si $\forall a, b \in \mathbb{R}$ avec $ a \lt b$
$P(a \lt X \lt b) = \int_a^b f(x)~dx$.
Remarque 3. On se limitera aux variables aléatoires qui ont une densité de probabilité continue par morceaux.
Exemple 3. On laisse tomber une balle de tennis d'une hauteur de 1 mètre et on prend comme variable aléatoire $X$ la hauteur à laquelle la balle rebondit, exprimée en décimètres. La densité de probabilité de $X$ pourrait être la fonction
$f(x) = \begin{cases} \dfrac{-3x^2+48x-189}{4}~& \text{si}~7 \le x \le 9\\ ~0 & \text{sinon} \end{cases}$
dont le graphe est illustré à la figure 5.
Remarque 4. On a
$P(X=a)=P(X=b)=0$
et donc
$\begin{align} P(a \lt X \lt b) & = P(a \le X \lt b) \\ & = P(a \lt X \le b) = P(a \le X \le b). \end{align}$
3 Densités de probabilité : propriétés. Espérance et variance
Proposition 1. Soit $f$ la densité de probabilité d'une variable aléatoire continue $X$. On doit avoir
| i) | $f(x) \ge 0,~\forall x \in \mathbb{R}$; |
| ii) | $\int_{-\infty}^{\infty}f(x)~dx = 1$. |
Preuve : i) résulte du fait qu'une probabilité ne peut pas être négative. Quant à ii), c'est une conséquence de l'égalité
$\int_{-\infty}^{\infty}f(x) = P(X \in \mathbb{R})$.
Problème 1. Montrez que la densité de probabilité de l'exemple 3 vérifie les énoncés de la proposition 1.
Solution : i) $f(x) \ge 0$ car pour $x \in ]-\infty, 7[ \cup ]9, \infty[$, $f(x)=0$ et pour $x \in [7, 9]$, on peut vérifier que
$f(x) = \dfrac{3(x-7)(9-x)}{4} \ge 0$.
ii) On a
$\int_{-\infty}^{\infty}f(x)~dx = \dfrac{1}{4} \int_{7}^{9}\left(-3x^2+48x-189\right)~dx \\ ~~~~~~~~~~~~~~~~~~~~~= \dfrac{1}{4} \left[-x^3+24x^2-189x\right]_7^9 = 1.$
Définition 2. Soit $X$ une variable aléatoire de densité de probabilité $f$. On définit l'espérance $\mu$ de $X$ par la formule
$\mu = \int_{-\infty}^{\infty}xf(x)~dx$
et sa variance $\sigma^2$ par
$\sigma^2 = \int_{-\infty}^{\infty}(x-\mu)^2f(x)~dx$.
On dit que l'espérance d'une variable aléatoire $X$ est une
mesure de tendance centrale. Elle indique où se situe le « centre de gravité » des valeurs possibles de $X$.

La variance, elle, est qualifiée de mesure de dispersion. Elle indique si la variable aléatoire risque de prendre des valeurs plus proches ou plus éloignées de l'espérance.
Exemple 4. La variable aléatoire de l'exemple 3 a pour espérance $\mu = 8$ et pour variance $\sigma^2 = 0.2$.
Remarque 5. Si la fonction $f$ est nulle en dehors d'un intervalle borné, l'espérance et la variance existeront toutes les deux. Sinon, leur existence dépendra de la convergence des intégrales impropres qui les définissent (voir exercices 5 et 6)¹.
¹ Bien sûr, on ne peut pas définir la variance si l'espérance n'existe pas !
4 Vidéo
5 Exercices
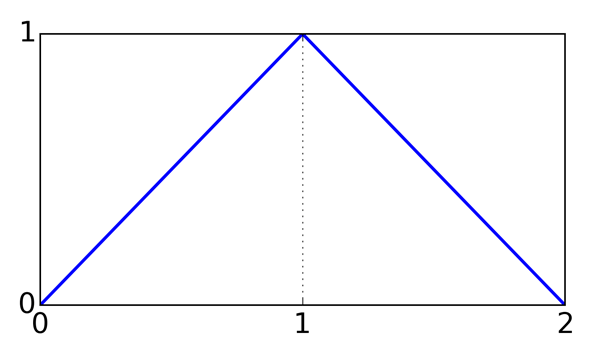
Exercice 1. La figure 8 reproduit une portion du graphe d'une fonction $f$ qui s'annule pour $x \lt 0$ et $x \gt 2$. Si $X$ est une variable aléatoire qui a $f$ comme densité de probabilité,
a) calculez $P(X \lt 0.6)$, $P(0.7 \lt X \lt 1.3)$ et $P(X \gt 1.8)$;
b) calculez l'espérance et la variance de $X$.
Exercice 2. On dit qu'une variable aléatoire suit une loi uniforme $U(a, b)$ si sa densité de probabilité est de la forme
$f(x) = \begin{cases} \dfrac{1}{b-a}~& \text{si}~a \le x \le b\\ ~0 & \text{sinon.} \end{cases}$
Calculez l'espérance et la variance d'une variable aléatoire qui suit une loi uniforme $U(0, 1)$.
Exercice 3. Effectuez les calculs pour l'exemple 4.
Suggestion : Montrez que pour $x \in [7, 9]$, on peut
écrire
$f(x) = \dfrac{3}{4} \left[ 1- (x-8)^2 \right]$.
Exercice 4. On dit qu'une variable aléatoire suit une loi exponentielle de paramètre $\lambda \gt 0$ si sa densité de probabilité est de la forme
$f(x) = \begin{cases} C e^{-\lambda x}~& \text{si}~x \ge 0\\ ~0 & \text{si} ~x \lt 0.\end{cases}$
Montrez qu'on doit avoir $C = \lambda$.
Exercice 5. Calculez l'espérance et la variance d'une variable aléatoire qui suit une loi exponentielle de paramètre $\lambda$. (N.B. vous devez montrer que les intégrales impropres convergent.)
Exercice 6. Une variable aléatoire $X$ a pour densité de probabilité la fonction
$f(x) = \dfrac{C}{x^2+1}$.
a) Trouvez la valeur de $C$.
b) Montrez que l'espérance de $X$ n'est pas définie.