Valeur moyenne d'une fonction

Nous allons voir dans cette page comment les intégrales peuvent être utilisées pour calculer la moyenne de phénomènes continus. Les concepts vus ici ont des applications dans divers domaines des sciences et du génie.

1 Valeur moyenne d'une fonction continue

Lorsqu'on a une suite de $n$ valeurs discrètes $X_1$, $X_2$, …, $X_n$, on sait comment définir leur moyenne : elle est donnée par la formule

$\left< X \right>=\dfrac{\sum_{k=1}^n X_k}{n}$.

Mais il existe des cas où le phénomène étudié est une quantité qui varie de manière continue.

Comment peut-on, par exemple, définir la température moyenne à Moncton en juin, la moyenne annuelle de la hauteur de la marée dans la baie de Shédiac, etc. ? On veut ici prendre des moyennes de quantités $f(t)$ où la variable $t$ varie continûment dans un certain intervalle $[a, b]$ (le mois de juin, l'année 2017, … ).

La première idée qui vient à l'esprit est d'échantillonner la quantité en question et de prendre la moyenne des échantillons. Par exemple, à Moncton, on va mesurer le température toutes les heures durant le mois de juin : ça va nous donner 30 × 24 = 720 mesures de température dont on peut alors prendre la moyenne. Évidemment, le résultat sera plus précis si on échantillonne toutes les minutes, ou, encore mieux, toutes les secondes.

Le principe est donc le suivant : on divise l'intervalle $[a, b]$ en $n$ sous-intervalles de largeur $\Delta t=(b-a)/n$, dans chacun des sous-intervalles, on prend un échantillon $f(t_k^*)$ et on calcule une moyenne approximative

$\left< f \right>_{[a, b]} \approx\dfrac{\sum_{k=1}^n f(t_k^*)}{n}=\dfrac{\sum_{k=1}^n f(t_k^*)~\Delta t}{b-a}$.

En prenant la limite $n \rightarrow \infty$, on est conduit à la définition suivante :

Définition 1. Soit $f$ est une fonction continue sur un

intervalle $[a, b]$. On définit la moyenne de cette fonction sur l'intervalle par

$\left< f \right>_{[a, b]}=\dfrac{1}{b-a}\int_a^b f(t)~dt$.

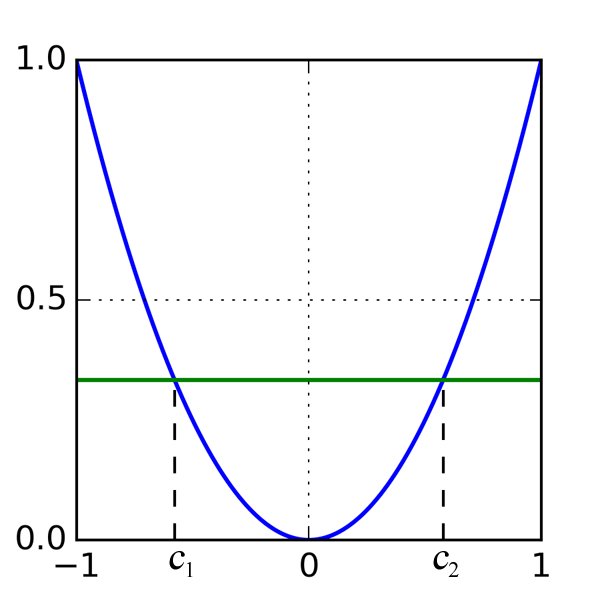
Exemple 1. Prenons la fonction $f(t)=t^2$. Sa moyenne sur l'intervalle $[-1, 1]$ est

$\left< f \right>_{[-1, 1]}=\dfrac{1}{2}\int_{-1}^1 t^2~dt=\dfrac{1}{2}\dfrac{2}{3}=\dfrac{1}{3}$.

Remarque 1. D'après la définition 1, on a

$\int_a^b f(t)~dt=\left< f \right>_{[a, b]}(b-a)$.

Cela veut dire que si la fonction $f$ est positive, l'aire de la surface délimitée par son graphe, l'axe des $x$ et les verticales $x=a$ et $x=b$ est la même que l'aire d'un rectangle de base $b-a$ et de hauteur $\left< f \right>_{[a, b]}$ (voir figure 1).

Fig. 1. Au-dessus de l'intervalle $[-1, 1]$, l'aire de la surface sous la courbe $y=t^2$ et l'aire de la surface sous la droite horizontale $y=1/3$ sont égales.

2 Deux résultats intéressants

Il y a deux résultats intéressants concernant les valeurs moyennes des fonctions. Le premier est souvent présenté comme le « théorème de la valeur moyenne ». Il s'agit en fait d'une version « calcul intégral » du théorème des accroissements finis.

Proposition 1. Soit $f$ est une fonction continue sur un intervalle $[a, b]$. Il existe $c \in ]a, b[$ tel que

$f(c)=\left< f \right>_{[a, b]}$.

Preuve. Le théorème fondamental du calcul différentiel et intégral nous dit que la fonction $F$ définie par

$F(t)=\int_a^t f(t')~dt'$

est continue sur $[a, b]$ et dérivable sur $]a, b[$ avec $F'(t) = f(t)$; de plus, on a

$F(a)=0,~~F(b)=\int_a^b f(t)~dt$.

D'après le théorème des accrois­sements finis, il doit exister $c \in ]a, b[$ tel que

$F'(c)=\dfrac{F(b)-F(a)}{b-a}$

donc tel que

$f(c)=\dfrac{1}{b-a}\int_a^b f(t)~dt=\left< f \right>_{[a, b]}$.

Fig. 2. Cas de l'exemple 1.

Exemple 2. Dans le cas de l'exemple 1, il y a deux valeurs possibles de $c$, qui sont les valeurs de $t$ où la droite $y=1/3$ coupe la para­bole $y=t^2$. On pourrait donc prendre comme valeur de $c$ soit $1/\sqrt{3}$, soit $-1/\sqrt{3}$.

Le deuxième résultat est relatif aux taux de variation :

Proposition 2. Soit $g$ une fonction continûment déri­vable sur un intervalle ouvert contenant $[a, b]$. On a

$\left< g'\right>_{[a, b]}=\dfrac{g(b)-g(a)}{b-a}$

c.-à-d. que le taux de variation moyen de $g$ sur $[a, b]$ est égal à la moyenne de son taux de variation instantané sur le même intervalle.

Preuve. Étant donné que $g$ est une primitive de $g'$, on a, d'après la formule de Newton-Leibniz

$\left< g' \right>_{[a, b]}=\dfrac{1}{b-a}\int_a^b g'(t)~dt=\dfrac{g(b)-g(a)}{b-a}$.

3 Vidéos

Vidéo #1. Valeur moyenne d'une fonction I.
Vidéo #2. Valeur moyenne d'une fonction II.

4 Exercices

Fig. 3. Graphique de la fonction $f$.

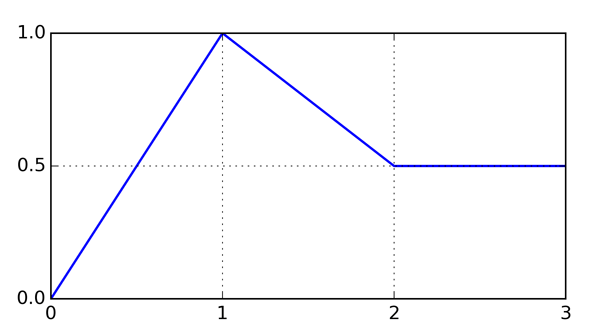
Exercice 1. a) Cal­culez les valeurs moyennes $\left< f \right>_{[0, 2]}$ et $\left< f \right>_{[0, 3]}$ pour la fonction $f$ de la figure 3.

b) Pour quelles valeurs $c$ a-t-on $f(c)=\left< f \right>_{[0, 2]}$ et $f(c)=\left< f \right>_{[0, 3]}$ ?

Exercice 2. Un train parcourt une distance de 150 km en trois heures. Montrez qu'à un moment donné, sa vitesse devait être exactement 50 km/h.

Exercice 3. Trouvez la valeur moyenne de la fonction

$f(t) = sin^2(\omega t)~~(\omega \ne 0)$

sur l'intervalle $[0, 2 \pi / \omega]$.

Exercice 4. Soit $f$ une fonction continue sur un intervalle $[a, b]$. Montrez que si $c$ est le point milieu de l'intervalle, alors

$\left< f \right>_{[a, b]}=\dfrac{\left< f \right>_{[a, c]}+\left< f \right>_{[c, b]}}{2}$.

Montrez qu'il existe des formules analogues si on découpe l'intervalle $[a, b]$ en trois ou quatre parties égales.

Accueil