Coefficients de Fresnel – Réflexion par un miroir
Nous utilisons ici le formalisme développé à la page précédente, qui nous permet de calculer de manière très simple les coefficients de Fresnel à l'interface de deux milieux et les coefficients de réflexion par un miroir. Puisque nous travaillerons maintenant avec plus d'un milieu, nous ajouterons des indices aux matrices $\kk{}\pm$ et $\bb\pm{}$ pour indiquer dans quel milieu elles sont calculées.
1. Coefficients de Fresnel
Supposons que nous soyons en présence de deux milieux linéaires non magnétiques, le milieu 1 à gauche et le milieu 2 à droite, l'interface entre les deux étant le plan $z=z_1$. Quand, dans un des milieux, un champ incident se propage vers l'interface, il va en résulter un champ réfléchi dans le même milieu et un champ transmis dans l'autre. Si au moins un de ces milieux est anisotrope, les champs réfléchi et transmis n'ont a priori aucune raison d'avoir la même polarisation que le champ incident : il faudra donc décrire tous ces champs avec des
j-vecteurs que nous appellerons $\boldsymbol\phi_{in}$, $\boldsymbol\phi_{re}$ et $\boldsymbol\phi_{tr}$.
Nous voulons trouver deux matrices 2×2 $\mat r$ et $\mat t$ telles que $$\begin{array} {ll} \boldsymbol\phi_{re} = \mat r \boldsymbol\phi_{in}, & \boldsymbol\phi_{tr} = \mat t \boldsymbol\phi_{in}. \end{array}$$ Ces matrices généralisent les coefficients de Fresnel scalaires du chapitre II et nous leur donnerons le même nom. Pour les calculer, on utilisera le fait que le b-vecteur $\boldsymbol\Phi(z)$ qui décrit les champs dans les deux milieux doit être continu au passage de l'interface.
Champ incident venant de la gauche
Lorsque le champ incident est un champ + venant de la gauche, le champ transmis est aussi un champ + et le champ réfléchi un champ -. On devra donc avoir $$\begin{split} \boldsymbol\Phi(z_1) & = \kk1+ \boldsymbol\phi_{in} + \kk1- \boldsymbol\phi_{re} \\ & = \kk2+ \boldsymbol\phi_{tr} \end{split} \tag 1$$ En multipliant l'équation (1) à gauche par $\bb1+$ et $\bb1-$, on obtient $$\begin{array} {l} \phi_{in} = \pp1+2+ \boldsymbol\phi_{tr}, \\ \phi_{re} = \pp1-2+ \boldsymbol\phi_{tr}, \end{array}$$ ce qui veut dire que¹ $$\mat t_{12} = [\pp1+2+]^{-1}. \tag {2a}$$ et que
$$\begin{split} \mat r_{12} & = \pp1-2+ \mat t_{12} \\ & = \pp1-2+ [\pp1+2+]^{-1}. \end{split} \tag {2b}$$
On peut tout aussi bien multiplier (1) par $\bb2+$ et $\bb2-$. On obtient alors $$\begin{array} {l} \pp2+1+ \boldsymbol\phi_{in} + \pp2+1- \boldsymbol\phi_{re} = \phi_{tr}, \\ \pp2-1+ \boldsymbol\phi_{in} + \pp2-1- \boldsymbol\phi_{re} = 0, \end{array}$$ ce qui conduit ಠ$$\mat r_{12} = -[\pp2-1-]^{-1} \pp2-1+ \tag {3a}$$ et à une expression plus compliquée pour $\mat t_{12}$ : $$\begin{split} \mat t_{12} = & \pp2+1+ + \pp2+1- \mat r_{12} \\ = & \pp2+1+ - \pp2+1- \times \\ & [\pp2-1-]^{-1} \pp2-1+. \end{split} \tag {3b}$$
Champ incident venant de la droite
On peut répéter le processus pour un champ incident venant de la droite. À ce moment, on aura en $z=z_1$ $$\begin{split} \boldsymbol\Phi(z_1) & = \kk 1 - \boldsymbol\phi_{tr} \\ & = \kk 2 - \boldsymbol\phi_{in} + \kk 2 + \boldsymbol\phi_{re}. \end{split} \tag 4$$
De nouveau, on peut multiplier l'équation (4) à gauche soit par $\bb2-$ et $\bb2+$, soit par $\bb1-$ et $\bb1+$. Dans le premier cas, on obtient $$\begin{array} {l} \pp2-1- \boldsymbol\phi_{tr} = \phi_{in}, \\ \pp2+1- \boldsymbol\phi_{tr} = \phi_{re}, \end{array}$$ ce qui donne $$\mat t_{21} = [\pp2-1-]^{-1} \tag {5a}$$ et
$$\begin{split} \mat r_{21} & = \pp2+1- \mat t_{21} \\ & = \pp2+1- [\pp2-1-]^{-1}. \end{split} \tag {5b}$$
Dans le second cas, on obtient tout d'abord $$\begin{array} {r} 0 = \pp1+2- \boldsymbol\phi_{in} + \pp1+2+ \boldsymbol\phi_{re}, \\ \phi_{tr} = \pp1-2- \boldsymbol\phi_{in} + \pp1-2+ \boldsymbol\phi_{re}, \end{array}$$ ce qui conduit à $$\mkern -30mu\mat r_{21} = -[\pp1+2+]^{-1} \pp1+2- \tag {6a}$$ et à $$\mkern -35mu \begin{split} \mat t_{21} = & \pp1-2- + \pp1-2+ \mat r_{21} \\ = & \pp1-2- - \pp1-2+ \times \\ & [\pp1+2+]^{-1} \pp1+2-. \end{split} \tag {6b}$$¹ L'indice $12$ indique qu'on a un champ incident qui se propage du milieu 1 vers le milieu 2.
² L'équivalence des formules (2) et (3) est démontrée plus bas.
2. Inversion du parcours lumineux
Le passage de champs + à des champs - et vice-versa ne suffit pas pour obtenir une inversion du parcours lumineux : il faut en plus inverser la composante $x$ du vecteur d'onde, c'est-à-dire remplacer $\ka_x$ par $-\ka_x$. On utilisera un « prime » pour désigner les quantités calculées avec ce changement.
Si on note $\boldsymbol\Delta_k$ la valeur de la matrice $\boldsymbol\Delta$ dans le milieu $k$, on vérifie facilement que $$\boldsymbol\Delta_k^\prime = -\mat T \boldsymbol\Delta_k \mat T^{-1}, \tag {7a}$$ où $$\mat T = \mat T^{-1} = \diag(1, -1, 1, -1). \tag {7b}$$ Il résulte de ce fait que si $$\boldsymbol\Delta_k |~k, i \gt = \zeta_{k,i} |~k, i \gt, \tag {8a}$$ alors $$\boldsymbol\Delta_k^\prime \mat T |~k, i \gt = -\zeta_{k,i} \mat T |~k, i \gt. \tag {8b}$$ En renumérotant les vecteurs propres de manière adéquate, on peut s'arranger pour que
et
$$\bb k\pm^\prime = \bb k\mp \mat T^{-1} \tag {9b}$$Ces relations permettent de déduire des formules (2) et (6) que $$\mat t_{12}^\prime = [\pp1-2-]^{-1}, \tag {10a}$$ $$\mat r_{12}^\prime = \pp1+2- [\pp1-2-]^{-1} \tag {10b}$$ et que $$\mkern -30mu\mat r_{21}^\prime = -[\pp1-2-]^{-1} \pp1-2+ \tag {11a}$$ $$\mkern -35mu \begin{split} \mat t_{21}^\prime = & \pp1+2+ - \pp1+2- \times \\ & [\pp1-2-]^{-1} \pp1-2+. \end{split} \tag {11b}$$ On pourrait obtenir des formules équivalentes à partir des équations (3) et (5), comme par exemple $$ \mat r_{21}^\prime = \pp2-1+ [\pp2+1+]^{-1}, \tag {12a}$$ $$\mat t_{21}^\prime = [\pp2+1+]^{-1}. \tag {12b}$$
Principe du « retour inverse de la lumière »
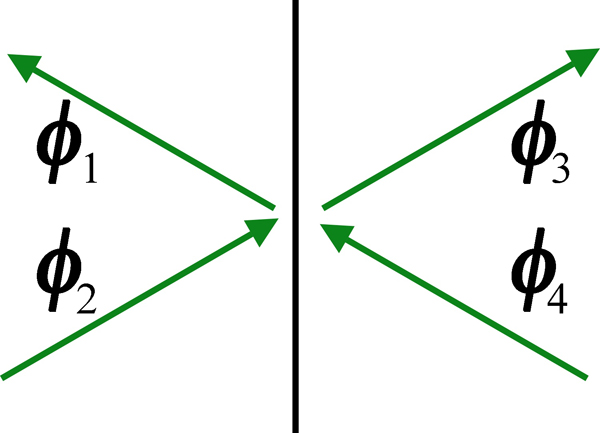
La figure à gauche illustre des champs incidents et réfléchis-transmis dans des milieux 1 et 2 séparés par une interface en $z=z_1$. On aura $$\begin{split} \boldsymbol\Phi(z_1) & = \kk1- \boldsymbol\phi_{1} \mkern 2mu + \kk1+ \boldsymbol\phi_{2} \\ & = \kk2+ \boldsymbol\phi_{3} \mkern 2mu + \kk2- \boldsymbol\phi_{4}. \end{split} \tag{13a}$$ avec $$\begin{array} {ll} \boldsymbol\phi_{1} = \mat r_{12} \boldsymbol\phi_{2} \mkern 2mu + \mat t_{21} \boldsymbol\phi_{4}, & \boldsymbol\phi_{3} = \mat r_{21} \boldsymbol\phi_{4} + \mat t_{12} \boldsymbol\phi_{2}. \end{array}$$ En multipliant l'équation (13a) par $\mat T$, on obtient $$\begin{split} \mat T \boldsymbol\Phi(z_1) & = \kk1+^\prime \boldsymbol\phi_{1} \mkern 2mu + \kk1-^\prime \boldsymbol\phi_{2} \\ & = \kk2-^\prime \boldsymbol\phi_{3} \mkern 2mu + \kk2+^\prime \boldsymbol\phi_{4}~: \end{split} \tag{13b}$$ le signe de $\ka_x$ a changé et les champs incidents sont
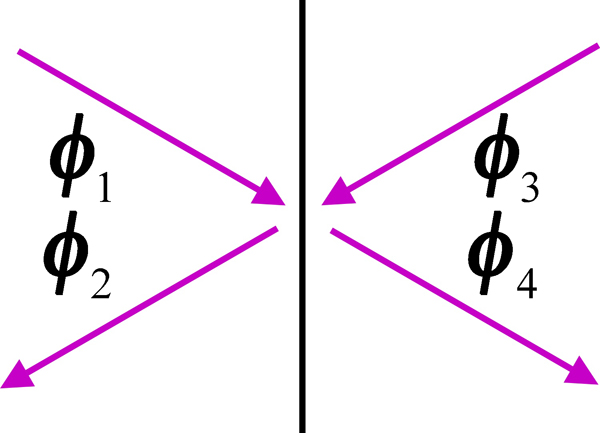
devenus des champs réfléchis-transmis et vice-versa. L'équation (13b) implique que $$\begin{array} {l} \boldsymbol\phi_{2} = \mat r_{12}^\prime \boldsymbol\phi_{1} + \mat t_{21}^\prime \boldsymbol\phi_{3}, \\ \boldsymbol\phi_{4} = \mat r_{21}^\prime \boldsymbol\phi_{3} + \mat t_{12}^\prime \boldsymbol\phi_{1}, \end{array}$$ ce qui est possible seulement si $$\begin{array} {ll} \mat t_{21}^\prime \mat t_{12} + \mat r_{12}^\prime \mat r_{12} = \mat I, & \mat t_{21}^\prime \mat r_{21} + \mat r_{12}^\prime \mat t_{21} = 0, \\ \mat t_{12}^\prime \mat t_{21} + \mat r_{21}^\prime \mat r_{21} = \mat I, & \mat t_{12}^\prime \mat r_{12} + \mat r_{21}^\prime \mat t_{12} = 0. \end{array} \tag {14a}$$ On peut montrer de manière similaire qu'on a aussi $$\begin{array} {ll} \mat t_{12} \mat t_{21}^\prime + \mat r_{21} \mat r_{21}^\prime = \mat I, & \mat t_{12} \mat r_{12}^\prime + \mat r_{21} \mat t_{12}^\prime = 0, \\ \mat t_{21} \mat t_{12}^\prime + \mat r_{12} \mat r_{12}^\prime = \mat I, & \mat t_{21} \mat r_{21}^\prime + \mat r_{12} \mat t_{21}^\prime = 0. \end{array} \tag {14b}$$
Ces relations généralisent un résultat de Stokes pour les milieux isotropes.
3. Réflexion par un miroir métallique
Lorsqu'on a un miroir métallique en $z=z_1$, il suffit de supposer qu'un des milieux est un conducteur parfait. On aura alors simplement un champ incident et un champ réfléchi dans l'autre milieu. La condition aux limites est que les composantes tangentielles du champ électrique doivent s'annuler en $z=z_1$ : on peut l'exprimer comme $$\bb{}E \boldsymbol\Phi(z_1) = 0$$
en introduisant la matrice $$\bb{}E = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \end{bmatrix}, \tag {15a}$$ qui a la propriété que $$\bb{}E \boldsymbol\Phi = \begin{bmatrix} E_x & E_y \end{bmatrix}^\t. \tag {15b}$$
Milieu parfaitement conducteur à droite
Avec $$\boldsymbol\Phi(z_1) = \kk1+ \boldsymbol\phi_{in} + \kk1- \boldsymbol\phi_{re},$$ on devra avoir $$\pp{}E1+ \boldsymbol\phi_{in} + \pp{}E1- \boldsymbol\phi_{re} = 0,$$
Inversion du parcours lumineux
Si on change le signe de $\ka_x$, on a alors $$\boldsymbol\Phi(z_1) = \kk1+^\prime \boldsymbol\phi_{in} + \kk1-^\prime \boldsymbol\phi_{re},$$ c'est-à-dire $$\boldsymbol\Phi(z_1) = \mat T \kk1- \boldsymbol\phi_{in} + \mat T \kk1+ \boldsymbol\phi_{re}$$ où $\mat T$ est donné plus haut. La condition aux limites sera donc $$\mkern -20mu \bb{}E \mat T \kk1- \boldsymbol\phi_{in} + \bb{}E \mat T \kk1+ \boldsymbol\phi_{re} = 0$$
Milieu parfaitement conducteur à gauche
On a maintenant $$\boldsymbol\Phi(z_1) = \kk2- \boldsymbol\phi_{in} + \kk2+ \boldsymbol\phi_{re}.$$ La condition aux limites donne alors $$\pp{}E2- \boldsymbol\phi_{in} + \pp{}E2+ \boldsymbol\phi_{re} = 0$$
Si on inverse le parcours lumineux, par un raisonnement analogue à celui fait plus haut, on trouve $$\mat r_{21}^\prime = \mat r_{21}^{-1}.$$
4. Compléments, notes et références
Équivalence des équations (2) et (3)
On a $$ \pp2-2+ = \pp2-1+ \pp1+2+ + \pp2-1- \pp1-2+ = 0. \tag {19}$$ En multipliant (19) à gauche par $[ \pp2-1- ]^{-1}$ et à droite par $[ \pp1+2+ ]^{-1}$, on obtient la relation $$ \pp1-2+ [ \pp1+2+ ]^{-1} + [ \pp2-1- ]^{-1} \pp2-1+ = 0$$ qui montre l'équivalence de (2b) et (3a). On montre de manière similaire que $$ \pp2+1- [ \pp2-1- ]^{-1} + [ \pp1+2+ ]^{-1} \pp1+2- = 0. \tag {20}$$ En partant maintenant de $$\pp1+1+ = \pp1+2+ \pp2+1+ + \pp1+2- \pp2-1+= \mat I,$$ et en utilisant (20), on arrive à $$\begin{split} [\pp1+2+]^{-1} & = \pp2+1+ + [\pp1+2+]^{-1} \pp1+2- \pp2-1+ \\ & = \pp2+1+ - \pp2+1- [ \pp2-1- ]^{-1} \pp2-1+, \end{split}$$ ce qui montre l'équivalence de (2a) et (3b).
On montre de manière similaire l'équivalence des équations (5) et (6).
Inversion du parcours lumineux
Les résultats de la section 2 concernant la matrice $\boldsymbol\Delta$ ne font qu'exprimer le simple fait suivant : si on a $$\begin{array} {ll} \mat k \times Z_0 \fffmat H + \dfrac \omega c \boldsymbol\eps' \fffmat E = 0, & \mat k \times \fffmat E - \dfrac \omega c Z_0 \fffmat H = 0, \end{array} \tag {21}$$ où $\mat k = (\omega/c) \begin{bmatrix} \ka_x & 0 & \zeta \end{bmatrix}^\t$, alors on aura aussi $$\begin{array} {ll} (-\mat k) \times (-Z_0 \fffmat H) + \dfrac \omega c \boldsymbol\eps' \fffmat E = 0, & (-\mat k) \times \fffmat E - \dfrac \omega c (-Z_0 \fffmat H) = 0. \end{array} \tag {22}$$
Principe du « retour inverse de la lumière »
Étant donné la forme de la matrice $\boldsymbol\Delta_k^\prime$, on peut facilement montrer que $$ \dfrac d {dz} \boldsymbol\Phi_k(z) = i \dfrac \omega c \boldsymbol\Delta_k \boldsymbol\Phi_k(z)~~\Rightarrow~~ \dfrac d {dz} \boldsymbol\Phi_k^\prime(z) = i \dfrac \omega c \boldsymbol\Delta_k^\prime \boldsymbol\Phi_k^\prime(z),~\boldsymbol\Phi_k^\prime(z) = \mat T \boldsymbol\Phi_k(-z). \tag {23}$$