Une surface de révolution est la surface engendrée par la rotation d'une courbe (appelée génératrice) autour d'une droite (appelée axe de révolution). Nous nous intéresserons aux surfaces de révolution qui ont
un axe horizontal ou vertical et voulons calculer leur aire.
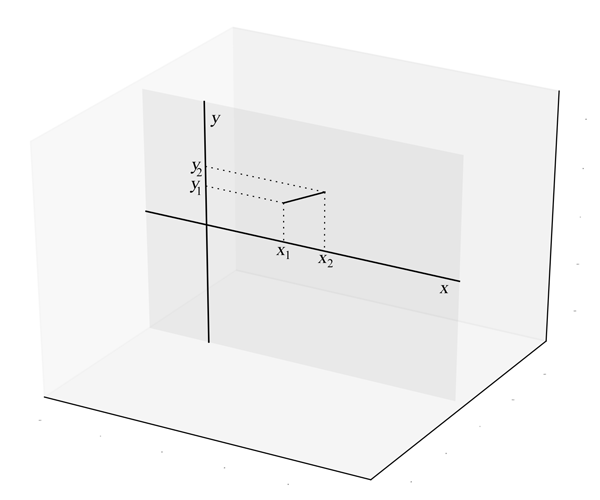
La surface de révolution la plus simple qu'on puisse envisager est celle qui a pour génératrice un segment de droite situé dans le demi-plan supérieur avec comme axe l'axe des $x$. Un tel segment est représenté
dans la figure 1. Nous désignerons les coordonnées de ses extrémités par $(x_1, y_1)$ et $(x_2, y_2)$.
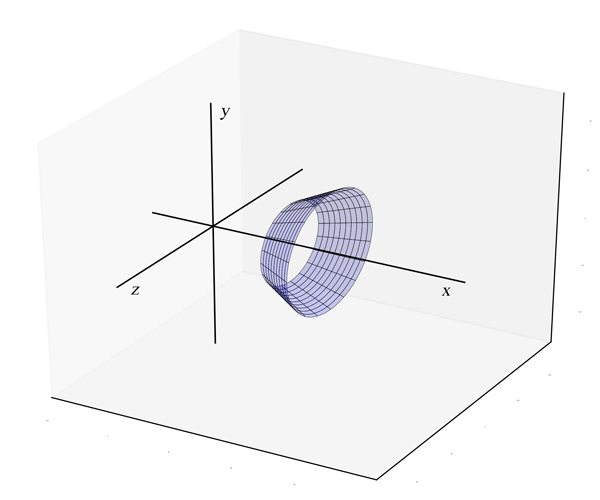
La figure 2 représente la surface de révolution obtenue en faisant tourner ce segment autour de l'axe des $x$. On constate qu'il s'agit de la surface latérale du solide de révolution obtenu
en faisant tourner la région délimitée par le segment, l'axe des $x$ et les verticales $x= x_1$ et $x=x_2$. Ce solide est un tronc de cône avec des bases circulaires de rayons respectifs $y_1$ et $y_2$.
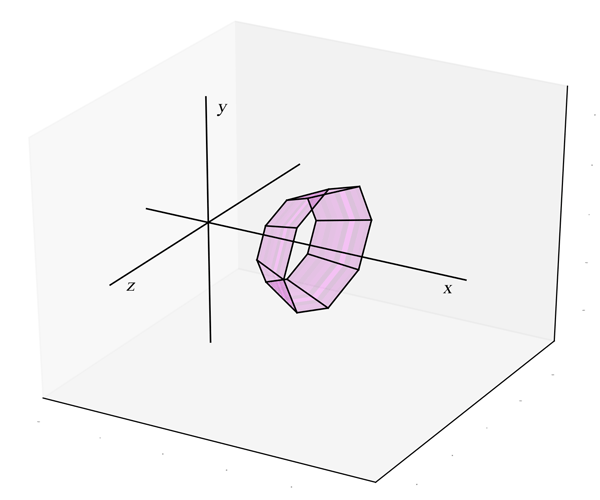
Nous voulons maintenant calculer l'aire de cette surface. Il y a plusieurs manières d'y arriver. Une des plus intuitives consiste à remarquer que la surface peut être approximée par une série de $n$ trapèzes égaux
(voir la figure 3). Si chacun de ces $n$ trapèzes a des bases de longueurs $a$ et $b$ et une hauteur $h$, cela donnera comme approximation de l'aire latérale du tronc de cône
$A \approx n \dfrac{a+b}{2} h$.
Il est clair en regardant la figure que si $n$ tend vers l'infini, $na$ et $nb$ vont tendre vers les circonférences respectives des deux bases, $2 \pi y_1$ et $2 \pi y_2$, alors que $h$ va tendre vers
la longueur $l$ du segment de droite. Ceci conduit à la formule
$A = \pi (y_1+y_2) l, ~~~l = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$.
Remarque 1. Cas particuliers : si les deux valeurs $y_1$ et $y_2$ sont égales, on retrouve la formule de l'aire pour la surface latérale d'un cylindre; si une des deux valeurs est nulle,
on obtient la formule pour l'aire de la surface latérale d'un cône.
Cas limite : si $x_1=x_2$, la formule donne l'aire d'un anneau.
Remarque 2. Si on fait tourner le segment autour de l'axe des $y$, en supposant qu'il est situé dans le demi-plan de droite, la formule devient
$A = \pi (x_1+x_2) l.$
Considérons maintenant une surface de révolution engendrée par la courbe
$y=f(x)~~~(a \le x \le b)$.
lorsqu'on la fait tourner autour de l'axe des $x$, en supposant que $f(x) \ge 0$ pour $x \in [a, b]$ et que $f$ est continûment dérivable. On veut calculer l'aire $A$ de cette surface.
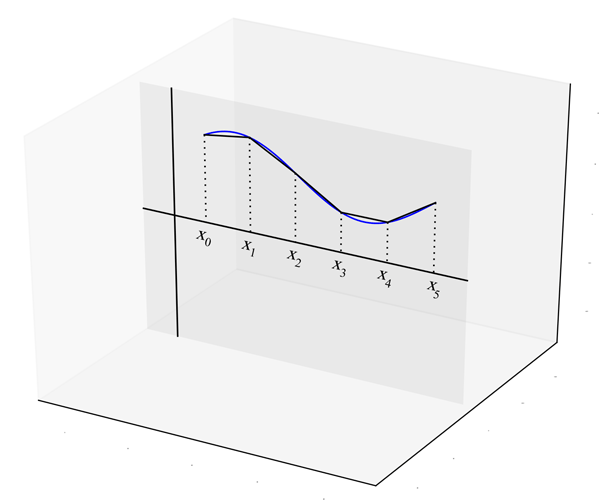
Tout comme on l'a fait pour calculer la longueur d'une courbe (voir page précédente), divisons l'intervalle $[a, b]$ en $n$ sous-intervalles $[x_{i-1}, x_i]$ de largeur égale $\Delta x = (b-a)/n$, avec $x_0 = a$ et $x_n = b$,
et approximons le graphe par la ligne brisée qui passe par les points $(x_i, f(x_i))$ (figure 4). La surface de révolution engendrée par le graphe (figure 5) sera d'autant mieux approximée par celle engendrée par
la ligne brisée (figure 6) que $n$ sera grand. Or, la seconde surface est formée de $n$ troncs de cône : on connait donc son aire. Ceci donne comme approximation de $A$ la valeur
$A \approx \sum_{i=1}^n \pi \left(f(x_{i-1})+f(x_i) \right) l_i$
où, en posant $\Delta y_i = f(x_i)-f(x_{i-1})$,
$l_i = \sqrt{\left(\Delta x \right)^2+ \left(\Delta y_i\right)^2} = \sqrt{1+\left(\dfrac{\Delta y_i}{\Delta x} \right)^2}\Delta x$.
Tout comme avant, avec nos hypothèses, on aura dans chacun des sous-intervalles i un point $x_i^*$ tel que $\Delta y_i = f'(x_i^*) \Delta x$. Si on fait l'approximation supplémentaire
$f(x_{i-1})+f(x_i) \approx 2f(x_i^*)$, on obtient au total
$A \approx \sum_{i=1}^n 2\pi f(x_i^*) \sqrt{1+\left(f'(x_i^*) \right)^2}\Delta x$.
Lorsqu'on fait tendre $n$ vers l'infini, cette expression a pour limite
$A = \int_a^b 2\pi f(x) \sqrt{1+\left(f'(x) \right)^2}~dx$.
Remarque 3. La formule peut aussi s'écrire
$A = \int_a^b 2\pi y \sqrt{1+(y')^2}~dx = \int_a^b 2\pi y \sqrt{1+\left(\dfrac{dy}{dx} \right)^2}~dx$.
Remarque 4. Pour une génératrice de la forme $x=g(y)$ $(c \le y \le d)$ où $g$ est continûment dérivable, l'aire de la surface engendrée en faisant tourner la courbe autour de l'axe des $y$ est
donnée la formule
$A = \int_c^d 2\pi g(y) \sqrt{1+\left(g'(y) \right)^2}~dy$.
Vous trouverez à la page suivante la suite de la matière sur les surfaces de révolution. Vous y trouverez aussi des vidéos sur le sujet et des exercices.